外部排序概念

对大文件进行排序，因为文件中的记录很多、信息量庞大，无法将整个文件复制到内存中进行排序

需要将带排序的记录存储在外存上，排序时再把一部分一部分地调入内存进行排序，在排序过程中需要多次进行内存和外存之间的交换

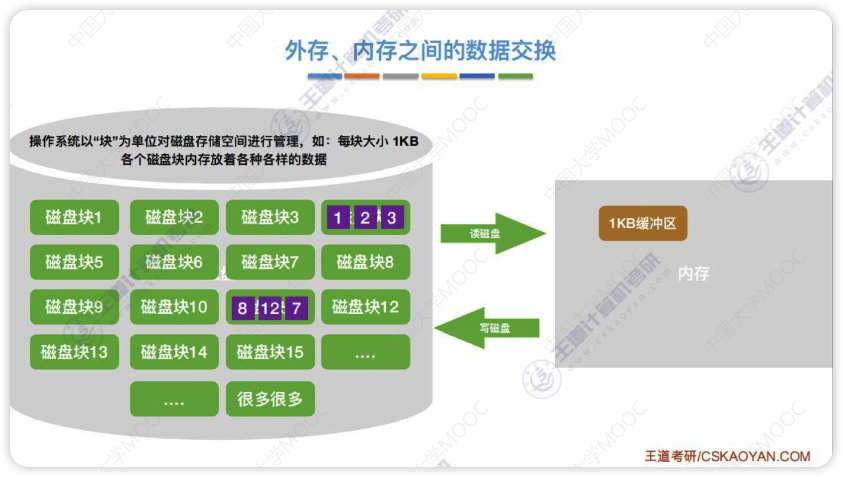
外部排序的方法

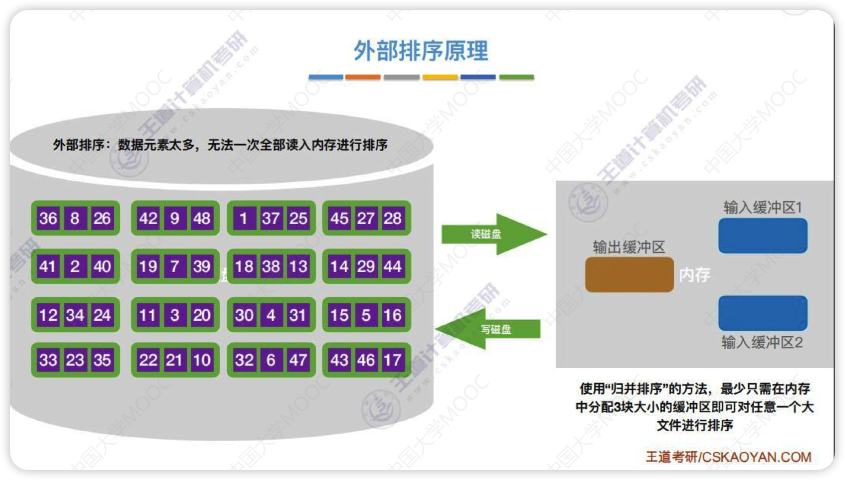
• 每次将外存中的两块(两个归并段)读到内存中的输入缓冲区
• 输入缓冲区进行排序，找到最小的依次放到输出缓冲区
• 输出缓冲区满了(有序子文件)就放回外存(放回去之后就是一个归并段)，输入缓冲区空了就从外存中读
• 内存外存之间的读写非常耗时，所以优化主要是考虑访问磁盘的次数，I/O次数
• 外部排序总时间=内部排序所需要的时间+外存信息读写时间(主要耗时)+内部归并所需时间

优化方式

优化主要考虑减少访问磁盘的次数

访问磁盘的次数=归并趟数$S=\lceil lo{g}_{k}r\rceil$$S=\lceil log_kr \rceil$

1. 增加k(归并路数)

   • 无脑增大只会增加内存消耗和内部排序的时间
   • 为了减少k增大刀子内部归并时比较次数增多的影响，可以使用败者树

2. 减少r(初始归并段个数)

   • 也就是每个初始归并段长一点
   • 可以使用置换-选择排序

3. 上一步如果使用置换-选择排序，会导致初始归并段的大小不同，可以优化初始归并段的顺序来降低访问磁盘的次数

   • 可以使用最佳归并树

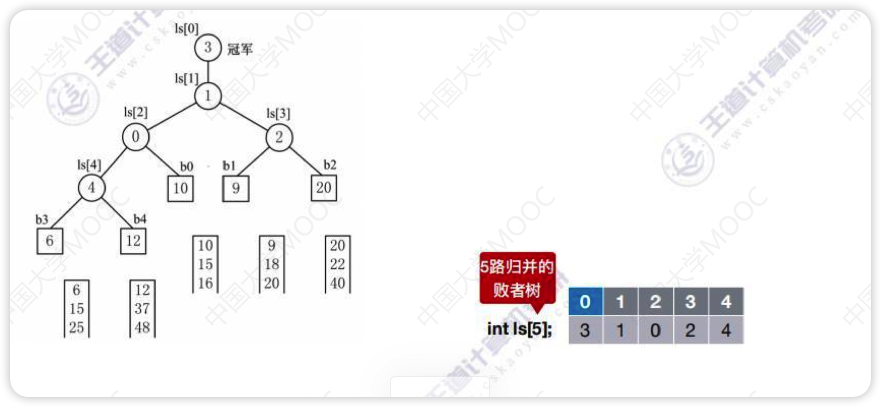
败者树

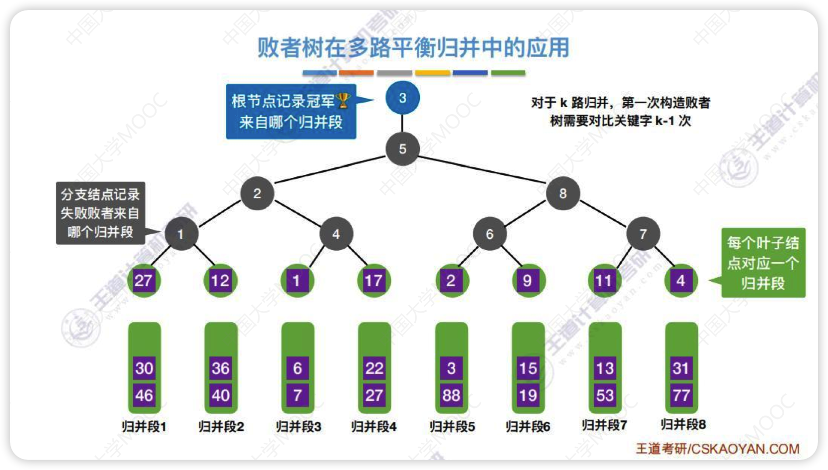
这种对战树就是败者树

• 败者树是一种特殊的完全二叉树(只不过多了个头)
• 不用败者树时每次找最小值都需要比较$k-1$$k-1$次，k是归并路数，使用败者树只需要$\lceil lo{g}_{2}k\rceil$$\lceil log_2k \rceil$次

置换-选择排序

• 主要用于生成初始归并段
• 原理：增加归并段的长度，减少初始归并段的数量，即减少r
• 置换-选择排序可以让每个初始归并段的长度超过内存工作区的大小

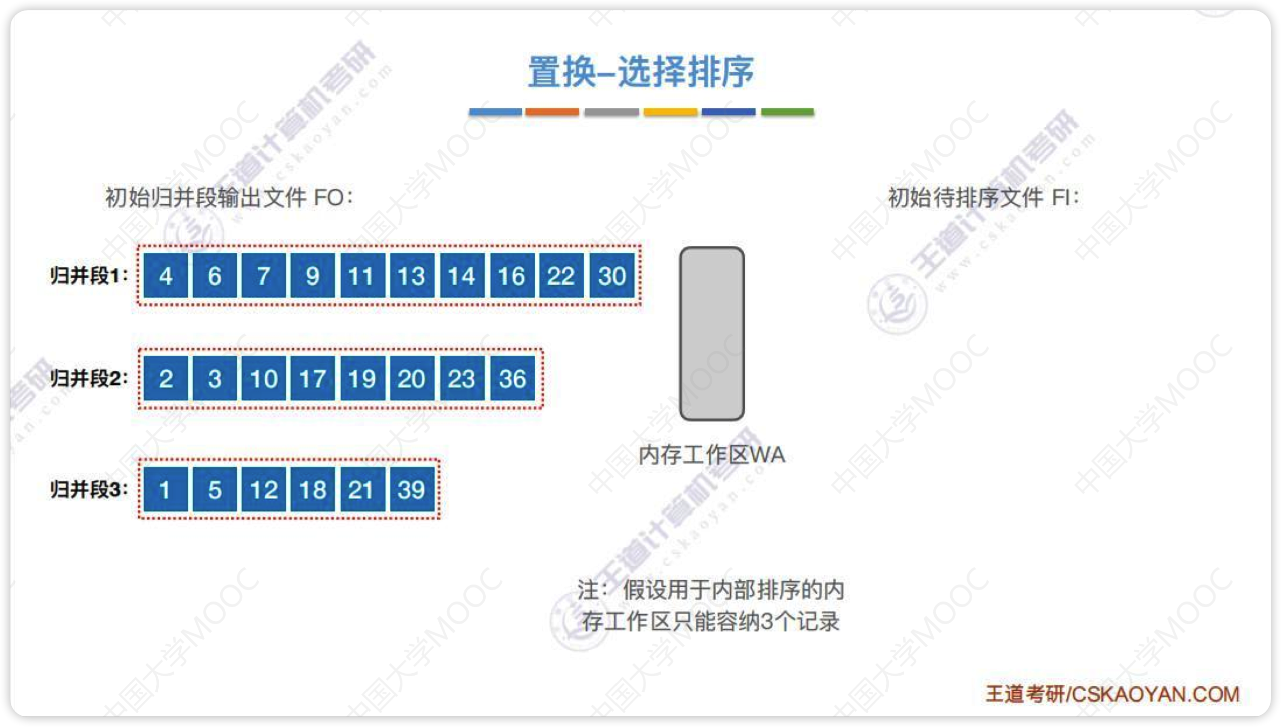
• 上面过程中的FI依然是一块一块的从外存中读入内存
• 输出FO依然是输出缓冲区，然后一块一块的存到外存

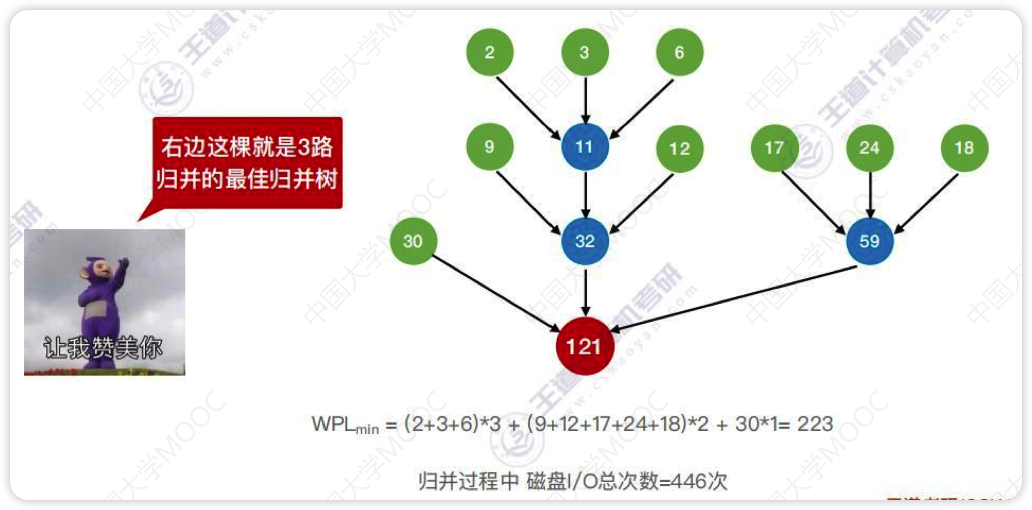
最佳归并树

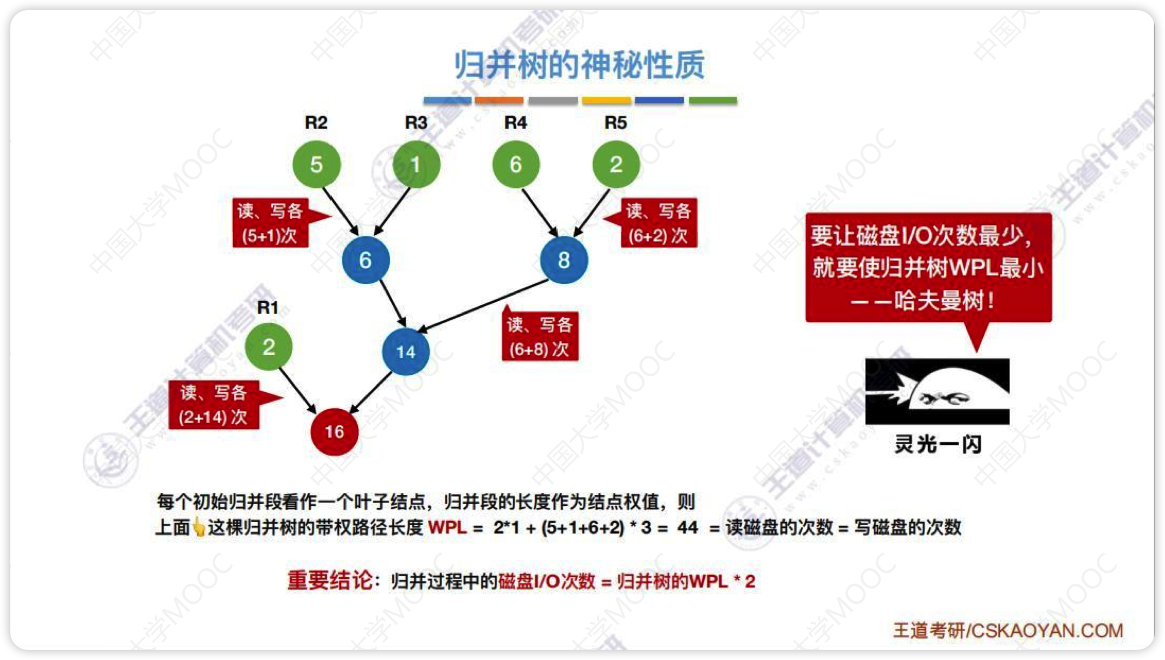
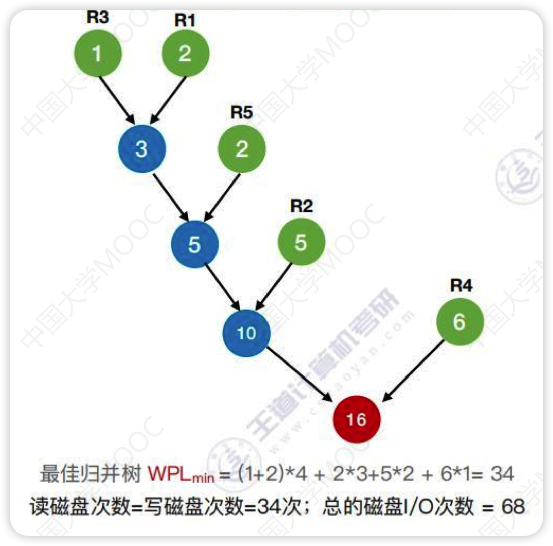
上图仅为2路归并时的最佳归并树，如果是多路归并则需要使用k叉哈夫曼树

• 归并过程中磁盘I/O次数 = 归并树的WPL*2

• 如果初始归并段不足以构成一棵严格k叉树时，需要添加长度为0的“虚段”(NULL)

  • 归并段不多的时候可以直接画一下，缺几个补几个

  • 设严格k叉树有n个结点，n₀个度为0的结点，n_k个度为k的结点

    • $n_0=(k-1)n_k+1$$n_0=(k-1)n_k + 1$=>$n_k=\frac{n_0-1}{k-1}$$n_k=\frac{n_0-1}{k-1}$
    • $(n_0-1)\mathrm{\%}(k-1)=0$$(n_0-1) \% (k-1) = 0$=>正好可以构造k叉归并树
    • $(n_0-1)\mathrm{\%}(k-1)=u\ne 0$$(n_0-1) \% (k-1) = u \not = 0$=>再加上$k-u-1$$k-u-1$个空归并段就可以建立归并树

• 

错题集

1. 

   答案与解析：

   
   答案： B
   解析：
   工作区能容纳600个记录=>一共有37500/600=625个归并段
   直接套公式可以$S=\lceil lo{g}_{m}r\rceil =\lceil lo{g}_{5}625\rceil =4$$S=\lceil log_mr \rceil=\lceil log_5625 \rceil=4$
   不会套公式可以一步步算
   第一趟归并排序会合并成625/5=125个归并段
   第二趟归并排序会合并成125/5=25个归并段
   第三趟归并排序会合并成25/5=5个归并段
   第四趟归并排序会合并成5/5=1个归并段
   

2. 

   答案与解析：

   
   答案： C B
   解析：
   传统顺序选(一个个比较)：每一次都要比较4次才能选出一个最小值，一共需要99次才能选完100个记录，所以总的比较次数为4*99=396次
   使用败者树：树高h=⌈log₂5⌉=3，每一次都需要比较3次才能选出一个最小值，一共需要比较100次，所以总的比较次数为3*100=300次