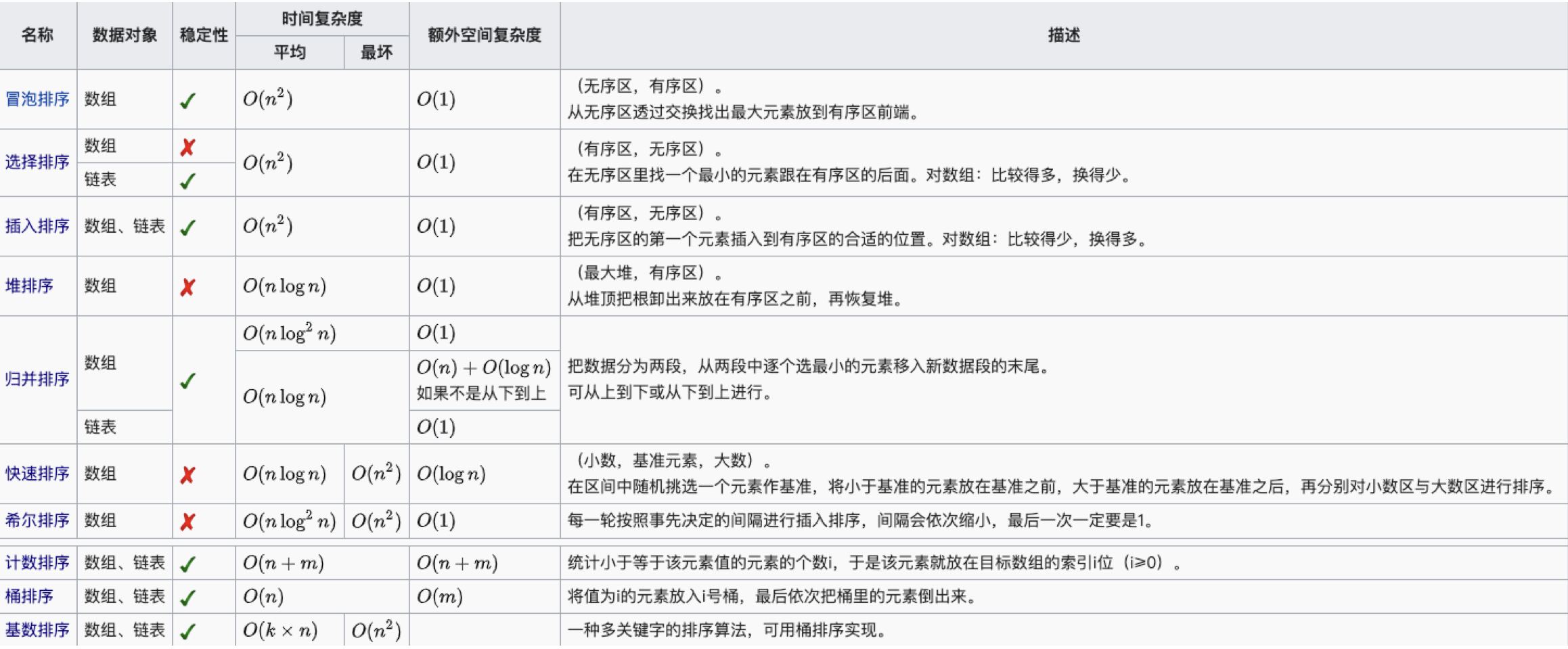
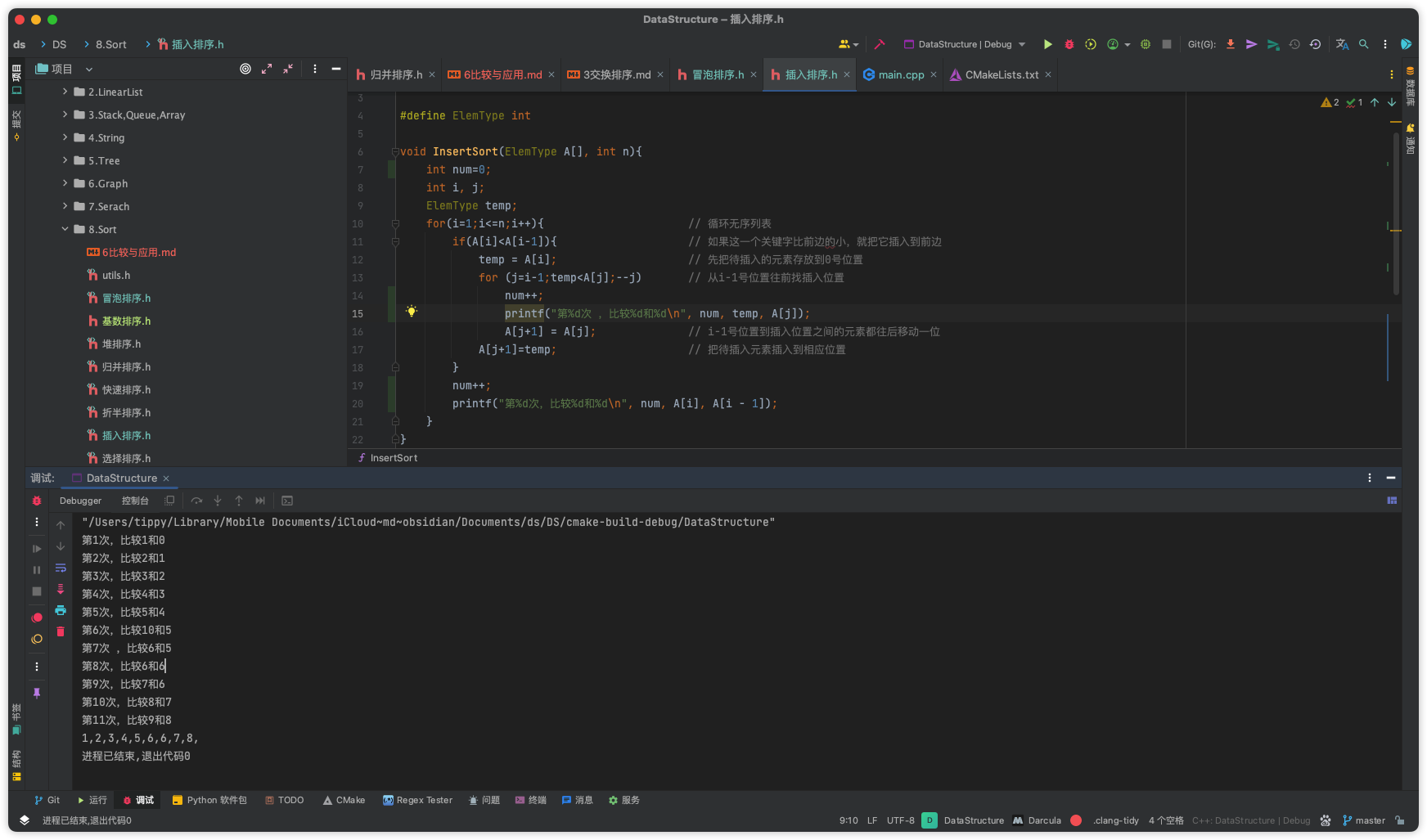
| 直接插入排序 | O(n) | O(n2) | O(n2) | O(1) | 稳定 | 内排序 | 数组、链表 | | - 可能出现:在最后一趟开始前,所有元素都不在最终位置
- 待排序序列基本有序的情况下,该方法效率最高
- 最坏情况比较次数=n(n-1)/2
- 最好情况比较次数=n-1
|
| 希尔排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 | 内排序 | 数组 | | |
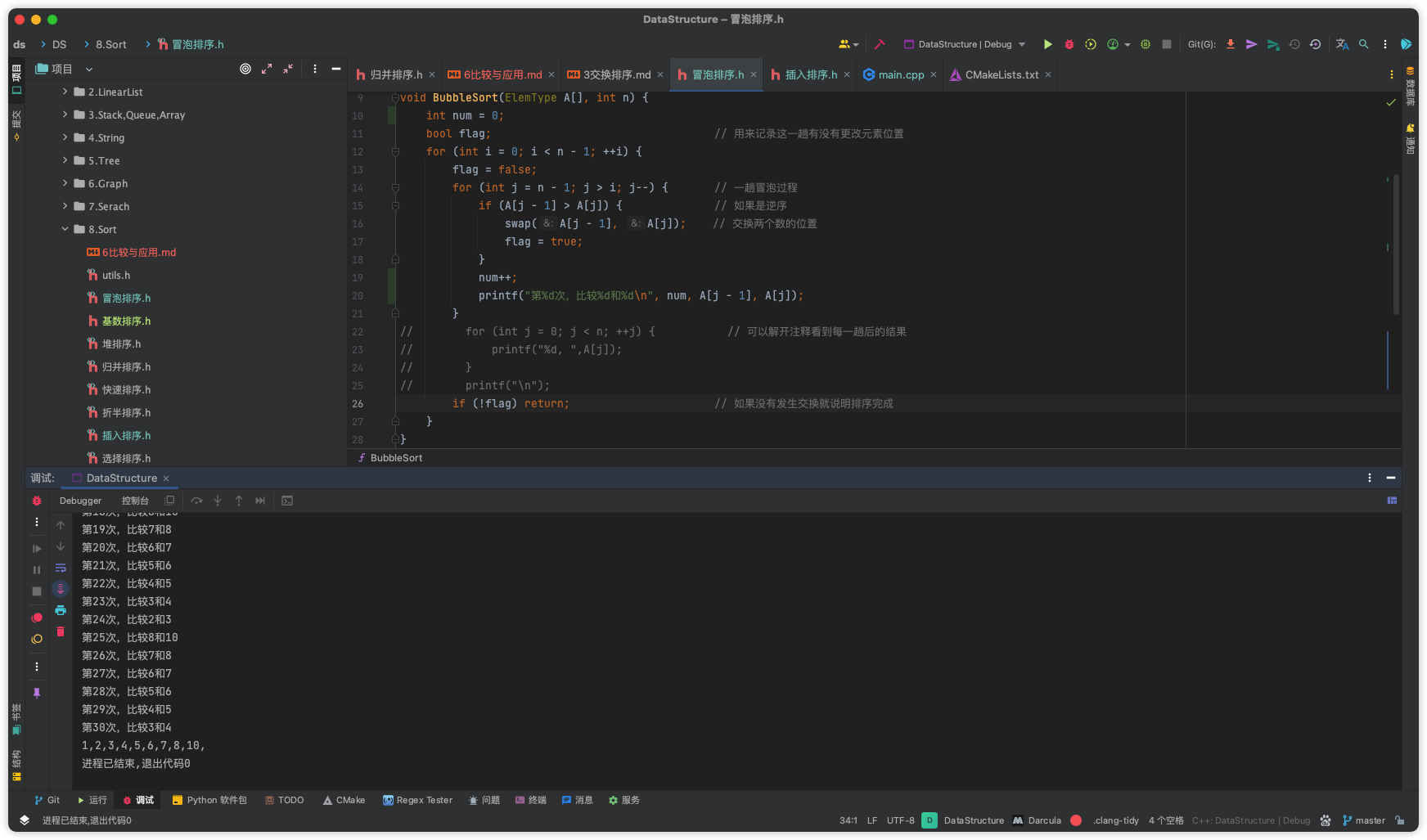
| 冒泡排序 | O(n) | O(n2) | O(n2) | O(1) | 稳定 | 内排序 | 数组 | | - 每一趟最后一个元素都是最大的元素(从小到大的序列)
- 元素从大到小时=最坏情况比较次数=n(n-1)/2
- 元素从小到大时=最好情况比较次数=n-1
|
| 快速排序 | O(nlog2n) | O(nlog2n) | O(n2) | O(nlog2n) | 不稳定 | 内排序 | 数组 | | - 蕴含了分而治之的思想
- 平均性能而言,目前最好的内部排序
- 当数据随机或者数据量很大的时候,适合快速排序;当排序的数据已基本有序,不适合快速排序
- 每次当枢轴把表分成等长部分时,速度最快
- 快速排序每趟都把基准元素放在最终位置(常用来计算是不是某一趟排序结果的题目,如第一趟至少有1个元素在最终位置,第二趟至少2个或3个在最终位置)
- 最大递归深度=枢轴值每次都将子表等分=树高位log2n
- 最小递归深度=枢轴值每次都是子表的最大值/最小值=单链表=树高为n
|
| 简单选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 | 内排序 | 数组、链表 | | |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 | 内排序 | 数组 | | - 取一大堆数据中k个最大(最小)的元素时,都优先采用堆排序
- 可以将堆视作一棵完全二叉树,采用顺序存储方式保护堆
- 插入和删除一个新元素的时间复杂度都是O(log2n)
- 构造n个记录的初始堆,时间复杂度为O(n)
|
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 | 外排序 | 数组、链表 | | - 分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n
- 比较次数数量级与序列初始状态无关
- 对于N个元素进行k路归并排序对趟数满足km=N
|
| 基数排序 | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O(r) | 稳定 | 外排序 | 数组、链表 | | - 通常基数排序第一趟按照个位数字大小,第二趟按照十位数字大小...
- MSD是最高位有限,LSD是最低位优先
- 基数排序不能对float和double类型的实数进行排序
|