散列表

基本概念

• 散列查找一般适用于关键字集合与地址集合之间存在对应关系的情况下的查找，是典型的"用空间换时间"的算法

• 散列查找的思想是计算出散列地址来查找，然后比较关键字以确定是否比较成功

• 散列函数：一个把查找表中的关键字映射成该关键字对应的地址的函数，记为 Hash(key) = Addr (Addr可以是索引、数组下标、地址等)

• 冲突：散列函数可能会把两个或两个以上的不同关键字映射到同一地址(这两个或几个关键字称为同义词)

  • 冲突是不可避免的，与装填因子无关

• 散列表：根据关键字而直接进行访问的数据结构(又叫Hash表，哈希表)

• 装填因子=表中记录数/散列表长度（参考下面构造方法中拉链法的例子）

• 散列表的平均查找长度与装填因子有关，与表长无关

• 为了提高查找效率，可以：

  • 设计冲突少的散列函数
  • 处理冲突时避免产生堆积现象（装填因子是固有属性，不可变）

• 产生了堆积(冲突)，对存储效率，散列函数和装填因子没什么影响，但ASL会随堆积现象而增大

构造方法

构造散列函数确定关键词存储位置 注意⚠️：

• 定义域包含全部需要存储的关键字
• 值域依赖于散列表的大小或地址范围
• 计算出来的地址应该能等概率、均匀的分布在整个地址空间中，从而减少冲突的发生
• 尽量简单，能在较短时间内计算出任一关键字对应的散列地址

散列函数：

• 直接定址法：

  • 直接取关键字的某个线性函数值为散列地址

  • H(key)=key或H(key)=a*key+b, (一元一次方程)

  • 特点

    • 计算简单且不会产生冲突
    • 适合关键字分布连续的情况
    • 如果不连续会使空位较多，造成存储空间的浪费

  • 比如用学生学号作为索引，散列函数就可以为学生学号-第一个学生的学号

• 除留余数法：

  • 假定散列表长为m，取一个小于等于m的最大质数p，用下面的公式转成散列地址

  • H(key)=key%p

  • 特点：

    • 最简单、最常用的方法
    • 关键是选好p，似的每个关键字通过该函数转换后等概率的映射到散列空间上的任一地址，从而尽可能减少冲突的可能性

• 数字分析法：

  • 设关键字是r进制数，而r个数码在各位上出现的频率不一定相同，可能在某位上分布均匀一些，每种数码出现的机会均等。而在某些位上分布不均匀，只有某几种数码经常出现，此时应选取数码分布较为均匀的若干为所为散列地址

  • 特点：

    • 适合于已知的关键字集合，若更换了关键字则需要构造新的散列函数

  • 比如某一城市居民的身份证号，可以只用后四位来构造

• 平方取中法：

  • 取关键字的平方值的中间几位作为散列地址

  • 特点：

    • 散列地址分布比较均匀
    • 适用于关键字的每位取值都不够均匀或均小于散列地址所需的位数
    • 这种方法得到的散列地址与关键字的每位都有关系

处理冲突

• 拉链法：

  • 将相应位置上冲突的所有关键词存储在同一个单链表中

  • 空地址比较不算一次查找

  • 🌰例子：

    • 关键字序列：[19,14,23,1,68,20,84,27,55,11,10,79]

    • 散列函数：$h(key)=key\mathrm{\%}13$$h(key) = key \% 13$

    • 

    • $19\mathrm{\%}13=6$$19\%13=6$, $14\mathrm{\%}13=1$$14\%13=1$, $23\mathrm{\%}13=10$$23\%13=10$, $1\mathrm{\%}13=1$$1\%13=1$, $68\mathrm{\%}13=3$$68\%13=3$, $20\mathrm{\%}13=7$$20\%13=7$, $84\mathrm{\%}13=6$$84\%13=6$, $27\mathrm{\%}13=1$$27\%13=1$, $55\mathrm{\%}13=3$$55\%13=3$, $11\mathrm{\%}13=11$$11\%13=11$, $10\mathrm{\%}13=10$$10\%13=10$, $79\mathrm{\%}13=1$$79\%13=1$

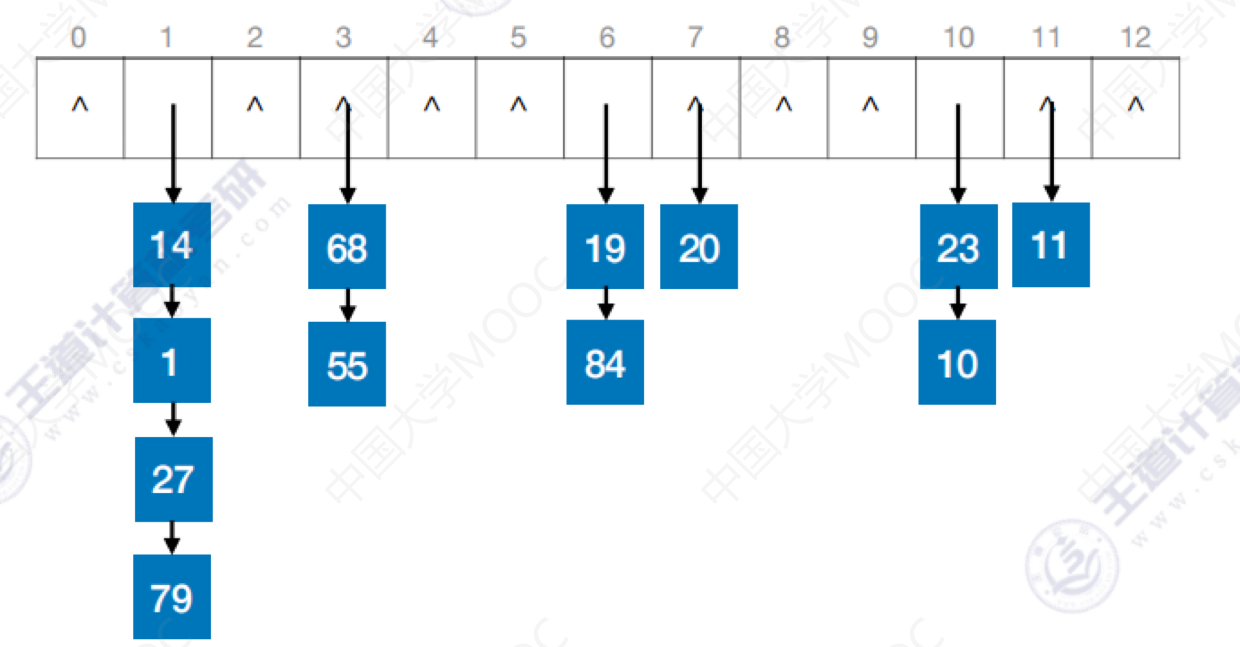
    • 查找成功的平均查找次数：$AS{L}_{\text{成}\text{功}}=(6\times 1+4\times 2+1\times 3+1\times 4)/12=1.75$$ASL_{成功}=(6\times1+4\times2+1\times3+1\times4)/12=1.75$

      • 表中有6个结点只需1次查找，4个结点需要2次查找，1个结点需要3次查找，1个结点需要4次查找

    • 查找失败的平均查找次数：$AS{L}_{\text{失}\text{败}}=(0+4+0+2+0+0+2+1+0+0+2+1+0)/13=0.92$$ASL_{失败}=(0+4+0+2+0+0+2+1+0+0+2+1+0)/13=0.92$

      • 这里分母的13是指散列函数mod后面的数字
      • 分子是每个结点处查找失败需要的比较次数
      • 结果被称为这个散列查找的装填因子

• 开放定址法：

  • 一旦产生了冲突，就按某种规则去寻找另一空地址

  • 发生聚集的原因主要是解决冲突的方法选择不当

  • 数学递推公式：$H_i=H(key)+d_i)\mathrm{\%}m$$H_i=H(key)+d_i) \% m$

  • 确定某一增量后使用的处理方法：

    • 线性探测法

      • $d_i=1,2,3,...,k(k\le m-1)$$d_i=1,2,3,...,k(k\leq m-1)$

      • 发生冲突时就按顺序往后找空闲位置放进去

      • 容易造成大量元素在相邻的散列地址上"聚集"（或堆积）起来

        • 出现堆积现象会导致平均查找长度增大
        • 堆积现象是由于同义词和非同义词之间发生冲突引起的

      • 🌰例子：

        • 长度为7的散列表, 插入[22, 43, 15, 30, 36], 散列函数$H(k)=k\mathrm{\%}7$$H(k)=k\%7$

        • 22 % 7=1 (1号位空着直接放入)

          22

        • 43 %7=1 (1号位已经放了元素所以放到2号位)

          22

          43

        • 15%7=1 (1号位已经放了元素就去找2号位，2号位也被占用所以放到3号位)

          22

          43

          15

        • 30%7=2 (这时候2号位置已经放了元素所以顺延查找3号位，3号位也被占用所以放到4号位)

          22

          43

          15

          30

        • 36%7=1 (1号位被占，查找后面的空位置是5号，所以放到5号位)

          22

          43

          15

          30

          36

    • 平方探测法

      • $d_i=0^2,1^2,-1^2,2^2,-2^2,...,k^2,-k^2,(k\le m/2)$$d_i=0^2,1^2,-1^2,2^2,-2^2,...,k^2,-k^2,(k \le m/2)$

      • 散列表的长度m必须是一个可以表示成4k+3的素数

        • 这样可以探测到整个散列表空间

      • 优点：可以避免堆积

      • 缺点：不能探测到散列表上所有单元，但至少能探测到一半单元（如果散列表长度不符合4k+3）

    • 双散列法

      • 有两个散列函数，第一个有冲突就换第二个
      • 最多经过m-1次探测就会遍历表中所有位置，回到H₀(初始探测位置)位置

ASL计算(线性探测法)

散列函数$H(key)=(key\times 3)\mathrm{mod}7$$H(key)=(key \times 3) \mod 7$ 计算散列函数值：

| key | 7 | 8 | 30 | 11 | 18 | 9 | 14 | | :——: | :——: | :——: | :——: | :——: | :——: | :——: | :——: | | H(key) | 0 | 3 | 6 | 5 | 5 | 6 | 0 |

散列表(线性探测法)

ASL_成功

$AS{L}_{\text{成}\text{功}}=\frac{1+1+1+1+3+3+2}{7}$$ASL_{成功} = \frac{1+1+1+1+3+3+2}{7}$

• 这里的7是指有7个元素

• 分子中的第一项：

  • 第一个元素7正好在0号位置，只需要比较一次

• 分子中的第五项：

  • 第五个元素18要查找5号位置，5号位置是11(比较一次)，再看6号位置，6号位置是30(比较第二次)，再看7号位置，7号位置是要找的值(比较第三次)
  • 这里比较三次所以是3

• 其他处理冲突方式的ASL_成功也是这样数成功查找到时需要比较的次数的总和比元素个数

ASL_失败

$AS{L}_{\text{失}\text{败}}=\frac{3+2+1+2+1+5+4}{7}$$ASL_{失败}=\frac{3+2+1+2+1+5+4}{7}$

• 分母的7是散列函数中mod后面的值

• 分子中第一项：

  • 在地址0查找失败的次数

  • 从0往后数到空的个数，0,1,2，一共三个，所以是3

    • 就是要比较0，1，2后才能说是查找失败

• 第六项：

  • 在地址5查找失败的次数
  • 从5往后数到空的个数，5,6,7,8,9，一共五个，所以是5

• 其他同理，因为mod7，所以查找时不会直接去查地址7及往后的位置，所以只需要算0-6的失败比较次数即可

• 其他处理冲突方式的ASL_失败也是分子为确定找不到时比较的次数的和，分母是mod后的值

错题集

1. 

   答案与解析：

   
   答案： C
   解析：
   

   0	1	2	3	4	5	6	7	8	9	10	11
   18	22	30	87	11	40	6	20

   ASL = (9+8+7+6+5+4+3)/7 = 6
   分子的每一项表示确定位置需要比较的次数
   比如9，指的是0号位的关键字需要比较0-8号后才能确定，需要比较9次
   分母表示散列函数能计算出的位置个数，这里只能算出0-6，也就是7个数