二叉排序树

• 当二叉树的叶子结点全部在相邻的两层时，深度最小。理想情况时从第一层到第二层是满二叉树 $h=\lceil lo{g}_{2}n+1\rceil$$h=\lceil log_2n+1 \rceil$
• 当输入序列是有序序列时，构造的二叉排序树是一支单支树，查找一个关键词最多需要比较n次
• 按中序遍历二叉排序树得到的是一个有序序列
• 二叉排序树中，关键字值最大的结点右指针一定为空

操作

• 查找

  • 

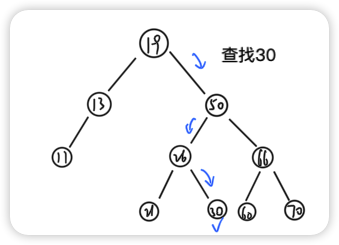
  • 递归查找

    • 最坏空间复杂度O(h) h是树高

      xxxxxxxxxx
      10
      1
      // 在二叉排序树查找值为key的结点（递归实现）  
      2
      BiNode *BSTSearch_recursion(BiTree T, int key) {  
      3
          if (T == nullptr)                                   // 二叉排序树中没有对应的值最后会变成空指针  
      4
              return NULL;  
      5
          if (key == T->data.value)                           // 找到对应值为key的结点，返回当前结点  
      6
              return T;  
      7
          if (key < T->data.value)                            // 要搜索的值比当前结点的值小，搜索左子结点  
      8
              return BSTSearch_recursion(T->lchild, key);  
      9
          return BSTSearch_recursion(T->rchild, key);     // 要搜索的值比当前结点的值大，搜索右子结点  
      10
      }
      

  • 顺序查找

    • 最坏空间复杂度O(1)

      xxxxxxxxxx
      11
      1
      // 在二叉排序树查找值为key的结点  
      2
      BiNode *BSTSearch(BiTree T, int key) {  
      3
          while (T != nullptr && key != T->data.value) {  // 值等于key就会跳过循环内的操作直接返回对应结点  
      4
              if (key < T->data.value)                    // 要搜索的值比当前结点的值小，指针变成左子结点  
      5
                  T = T->lchild;  
      6
              else                                        // 要搜索的值比当前结点的值大，指针变成右子结点  
      7
                  T = T->rchild;  
      8
          }  
      9
      
      10
          return T;
      11
      }
      

• 插入

  • 

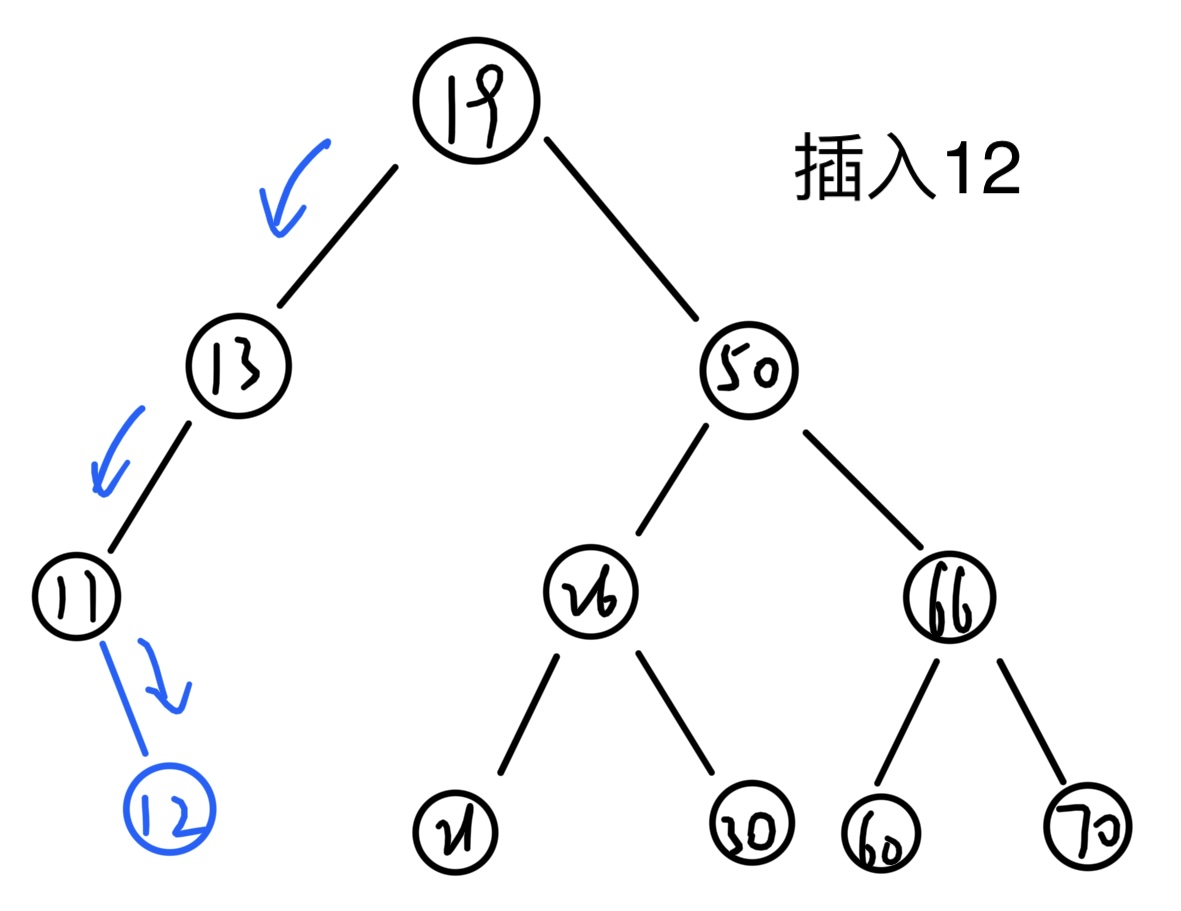
    xxxxxxxxxx
    14
    1
    // 向二叉排序树T中插入key  
    2
    int BSTInsert(BiTree &T, int key) {  
    3
        if (T == NULL) {  
    4
            T = (BiTree) malloc(sizeof(BiNode));     // 如果结点为空就新建一个结点  
    5
            T->data = {key};  
    6
            T->lchild = T->rchild = NULL;  
    7
            return 1;  
    8
        }  
    9
        if (key == T->data.value)                          // 如果存在一个一样的结点就跳过  
    10
            return 0;  
    11
        if (key < T->data.value)                           // 如果要插入的值key比当前结点的值小就插入左子结点  
    12
            return BSTInsert(T->lchild, key);  
    13
        return BSTInsert(T->rchild, key);               // 如果要插入的值key比当前结点的值大就插入右子结点  
    14
    }
    

• 构造

  • 按[50,66,60,26,21,30,70,68]建立BST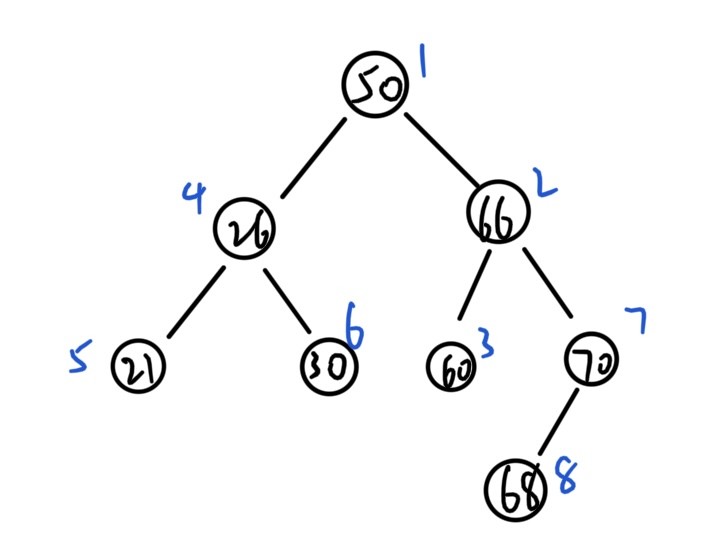

    • 

      xxxxxxxxxx
      5
      1
      void CreatBST(BiTree &T, int arr[], int n) {  
      2
          T = NULL;  
      3
          for (int i = 0; i < n; ++i)  
      4
              BSTInsert(T, arr[i]);  
      5
      }
      

• 删除

  • 

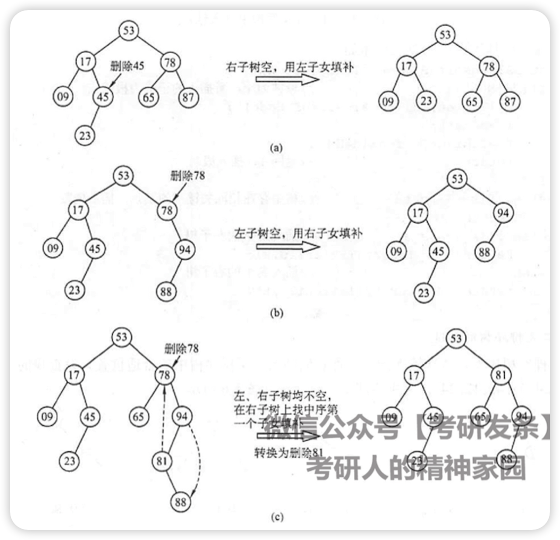
  • 一边空就用另一边补

  • 两边都不空就用右子树最小的（左下角）补上，同时删除右子树最小的结点

    xxxxxxxxxx
    24
    1
    // 在二叉排序树中删除值为key的结点  
    2
    BiNode *BSTDelete(BiTree &T, int key) {  
    3
        if (T == NULL)                                              // 没有要被删除的结点  
    4
            return NULL;  
    5
        if (key == T->data.value) {                                 // 找到要被删除的结点  
    6
            BiNode *biNode = T;                                         // biNode用来存放要被删除的结点  
    7
            if (T->lchild == NULL)                                      // 左子树为空就把当前结点变成右子结点  
    8
                T = T->rchild;  
    9
            else if (T->rchild == NULL)                                 // 右子树为空就把当前结点变成左子结点  
    10
                T = T->lchild;  
    11
            else {                                                      // 左右子树都不为空就把右子树的最小结点放到当前结点位置，删除右子树最小结点  
    12
                BiNode *low = T;                                            // low用来存放右子树最小结点  
    13
                while (low->lchild != NULL)                                 // 右子树左下角为最小结点  
    14
                    low = low->lchild;  
    15
                T = BSTDelete(low, low->data.value);                // 删除右子树最小结点，并将当前位置变为右子树最小结点  
    16
                T->lchild = biNode->lchild;                                 // 当前结点的左右子树指针修改为原结点指针  
    17
                T->rchild = biNode->rchild;  
    18
            }  
    19
            return biNode;  
    20
        }  
    21
        if (key < T->data.value)                                    // 要删除的值比当前结点值小，去左子树找  
    22
            return BSTDelete(T->lchild, key);  
    23
        return BSTDelete(T->rchild, key);                       // 要删除的值比当前结点值大，去右子树找  
    24
    }
    

查找效率分析

错题集

1. 

   答案与解析：

   
   答案： D
   解析：
   当二叉排序树所有结点都在一边时（单支树）查找比较次数最多，需要n次
   n>log₂n+1