图的存储
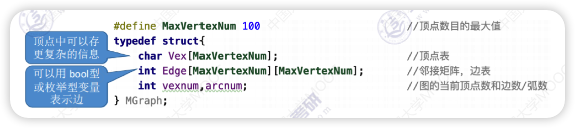
邻接矩阵法
用一个一位数组存储图中顶点的信息,用一个二维数组存储途中边的信息(即各顶点之间的邻接关系),存储顶点之间邻接关系的二维数组成为** 邻接矩阵**
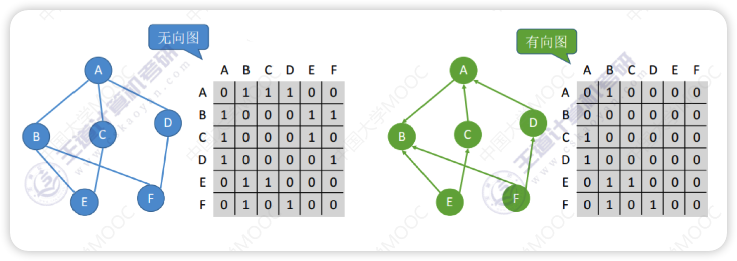
矩阵中只需要存放0和1(没有边和有边),可以更换bool型或者枚举型使矩阵更小
Vex中元素的位置与Edge中的行与列对应
- 无向图的邻接矩阵一定是关于斜对角线对称,压缩存储可以只存储上三角区/下三角区
- 求B元素的度可以找B所在行和列(对应出度和入度)的非0的个数
- 邻接矩阵法求顶点的度/出度/入度的时间复杂度为 O(|v|), v=顶点数
- 邻接矩阵法存储图的空间复杂度为 O(|v|2), v=顶点数
- 适合存储稠密图,稀疏图会浪费大量空间
如果是带权图,可以讲对应位置的 1 改为权值,用 ∞(int的上限值) 表示不存在边
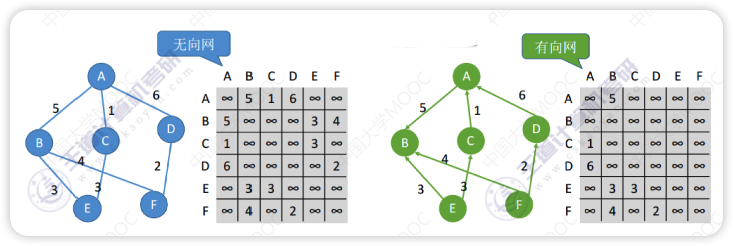 如果矩阵中的值是 ∞ 或 0,表示不存在边/弧
如果矩阵中的值是 ∞ 或 0,表示不存在边/弧
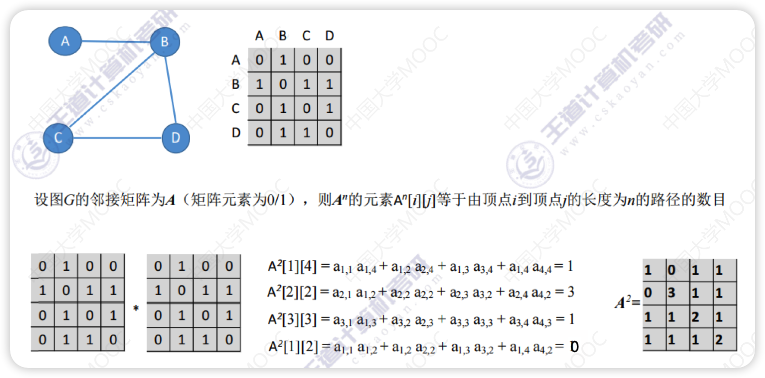
A2[1][4]
- 2指两步抵达,也就是上图等式中每一项都有两个数
- 1和4指从第一个元素到第4个元素(从1开始数),也就是等式中每一项第一个数的左坐标(行)是1,第二个数的右坐标(列)是4
- 计算后的数字就是路径的个数
邻接表法
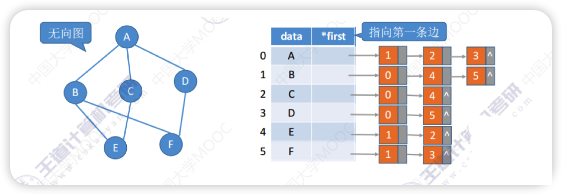
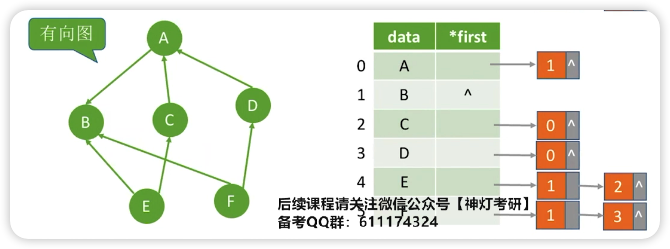
类似树的孩子表示法,是一个顺序链式表
- 无向图边结点的数量是2|E|,每条边在连接表中出现了两次,整体空间复杂度为O(|V|+2|E|)
- 有向图边结点数量是 |E|,整体空间复杂度为O(|V|+|E|)
- 有向图邻接表不方便寻找入度
- 图的邻接表不唯一,边结点的顺序结构可以改变(邻接矩阵唯一)
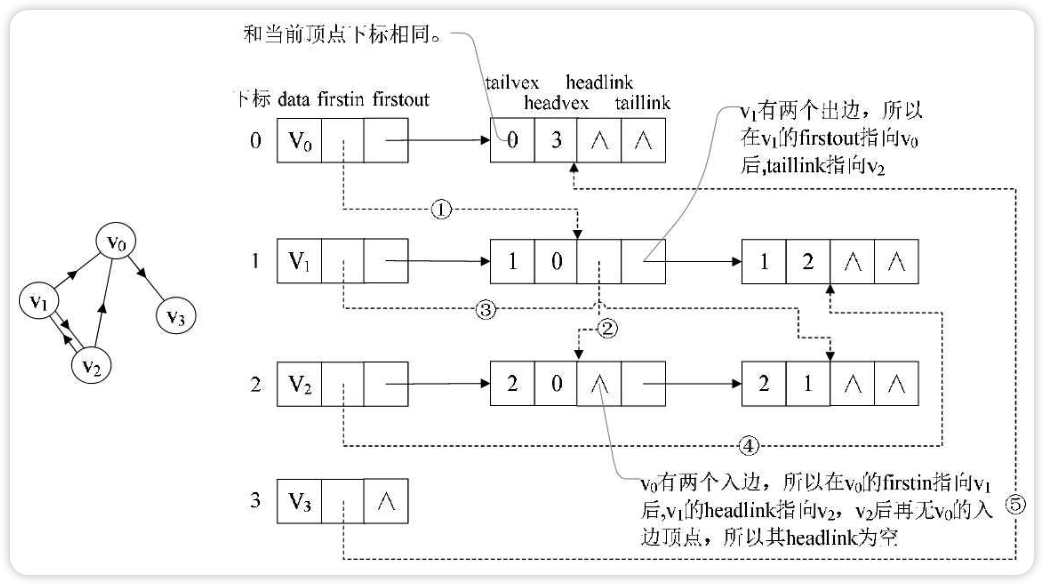
十字链表法(不用手写代码)
十字链表是有向图的一种链式存储结构。在十字链表中,对应于有向图中的每条弧有一个结点,对应于每个顶点也有一个结点(弧结点和顶点结点)。
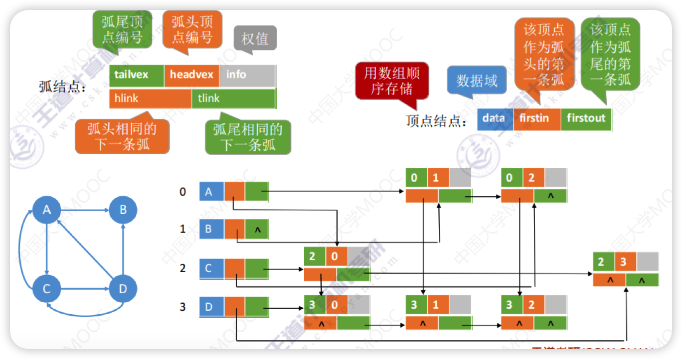
- 顶点结点的
firstin的链表长度就是该结点的入度 - 顶点结点的
firstout的链表长度就是该结点的出度 - 顺着绿色路线可以找到指定顶点的所有出边
- 顺着橙色路线可以找到指定顶点的所有入边
- 十字链表法只存储有向图
- 空间复杂度同邻接表,为 O(|V|+|E|)
如上图,顶点依然是存入一个一维数组{v0,v1,v2,v3}。就以顶点 v0 来说,firstout 指向的是出边表中第一个结点 v3。所以 v0 边表的 headvex=3,而 tailvex 其实就是当前顶点 v0 的下标 0,由于 v0 只有一个出边顶点,所以 headlink 和 taillink 都是空。
我们重点需要来解释虚线箭头的含义,他其实就是此图的逆邻接表的表示。对于 v0 来说,它有两个顶点 v1 和 v2 的入边。因此 v0 的 firstin 指向顶点 v1 的边表结点中 headvex 为 0 的结点,如图中的①。接着由入边结点的 headlink 指向下一个入边顶点 v2,如图中的②。对于顶点 v1,它有一个入边顶点 v2,所以它的 firstin 指向顶点 v2 的边表结点中 headvex 为 1 的结点,如图中的③。顶点 v2 和 v3 也是同样有一个入边顶点,如图中④和⑤。
---- 摘录自程杰老师的《大话数据结构》
邻接多重表(不用手写代码)
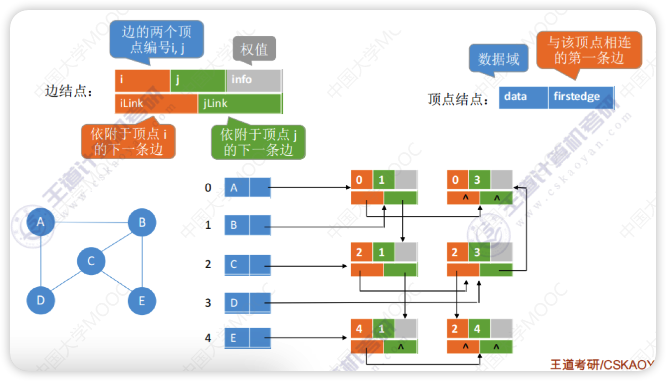
- 邻接多重表只存储无向图
- 与邻接表不同的是每条边只对应一份数据
- 空间复杂度为 O(|V|+|E|)
- 删除边、删除节点等操作很方便
对比
| 邻接表 | 邻接矩阵 | 十字链表 | 邻接多重表 | |
|---|---|---|---|---|
| 空间复杂度 | 无向图:O(|V|+2|E|) 有向图:O(|V|+|E|) | O(|V|2) | O(|V|+|E|) | O(|V|+|E|) |
| 适合用于 | 存储稀疏图 | 存储稠密图 | 只适用于有向图 | 只适用于无向图 |
| 表示方式 | 不唯一 | 唯一 | 不唯一 | 不唯一 |
| 删除边或顶点 | 无向图中删除边或顶点都不方便 | 删除边很方便,删除顶点需要大量移动数据 | 很方便 | 很方便 |
| 找相邻的边 | 找有向图的入边必须遍历整个邻接表 | 必须遍历对应行或列,时间复杂度为 O(|V|) | 很方便 | 很方便 |
图的基本操作
- Adjacent(G, x, y): 判断图 G 是否存在边<x, y>或(x, y)
- Neighbors(G, x): 列出图 G 中与结点 x 邻接的边
- InsertVertex(G, x): 在图 G 中插入顶点 x
- DeleteVertex(G, x): 从图 G 中删除顶点 x
- AddEdge(G, x, y): 若无向边(x, y)或有向边<x, y>不存在,则向图 G 中添加该边
- RemoveEdge(G, x, y): 若无向边(x, y)或有向边<x, y>存在,则从图 G 中删除该边
- FirstNeighbor(G, x): 求图 G 中顶点 x 的第一个邻接点,若有则返回顶点号,否则返回 -1
- NextNeighbor(G, x, y): 假设图 G 中顶点 y 是顶点 x 的一个邻接点,返回除 y 外顶点 x 的下一个邻接点的顶点号,若 y 是 x 的最后一个邻接点,则返回 -1
- Get_edge_value(G, x, y): 获取图 G 中边(x, y)或<x, y>对应的权值
- Set_edge_value(G, x, y, v): 设置图 G 中边(x, y)或<x, y>对应的权值为 v
错题集

答案与解析:
答案: D
解析:
有向图的邻接矩阵中,0和∞表示的都不是有向边 入度由列计算出,出度由行计算出
答案与解析:
答案: A
解析:
邻接表存储时,顶点数n决定了顶点表的大小,边数 e 决定了边表结点的个数