图的定义

图G由顶点集V和边集E组成，记为G=(V, E)

V(G)表示图G中顶点的有限非空集

E(G)表示图G中顶点之间的关系（边）的集合

若V = {v1,v2,v3,....,vn}，则用|v|表示图G中顶点的个数

若E = { (u,v) | u∈V, v∈ V }，用|E|表示G中边的条数

  1. 有向图

    有向图

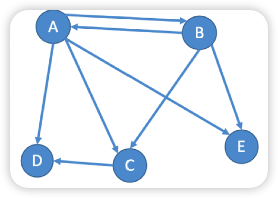
    • E 中的边都是有方向的，有向边也被称为弧

    • 弧是顶点的有序对，记为<v, w>，v是弧尾，w是弧头

    • <A,C>表示弧尾A到弧头C的弧，也称A邻接到C或C邻接自A

    • <A,B>≠<B,A>

    • 对于 n 个顶点的有向图 G

      • 所有顶点的出度之和=入度之和=|E|
      • 所有顶点的度之和=2|E|
      • 若 G 是强连通图，最少有 n 条边（形成回路）
      • 有向完全图共有 2C2n 条边

  2. 无向图

    无向图

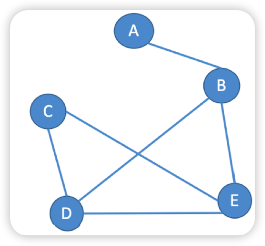
    • <A,B>=<B,A>

    • E中的边都是没有方向的，被称为边

    • 对于 n 个顶点的无向图 G

      • 所有顶点的度之和=2|E|
      • 若 G 是连通图，则最少有 n-1 条边（树），多于 n-1 就一定有回路
      • 若 G 是非连通图，最多可能有 C2n-1 条边
      • 无向完全图共有 2C2n 条边

  1. 简单图

    简单图

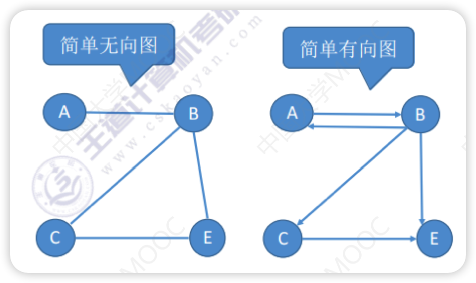
    • 不存在重复边
    • 不存在顶点到自身的边

  2. 多重图（了解即可）

    多重图

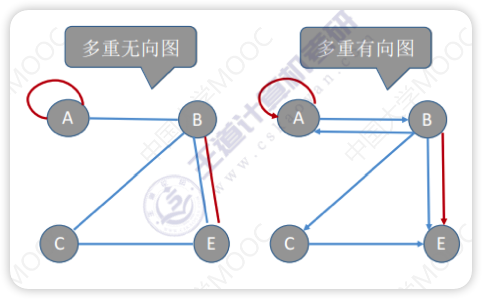
    • 与简单图相反，两个顶点之间的边数大于 1，允许顶点通过一条边与自己相连

  1. 完全图（简单完全图）

    完全图

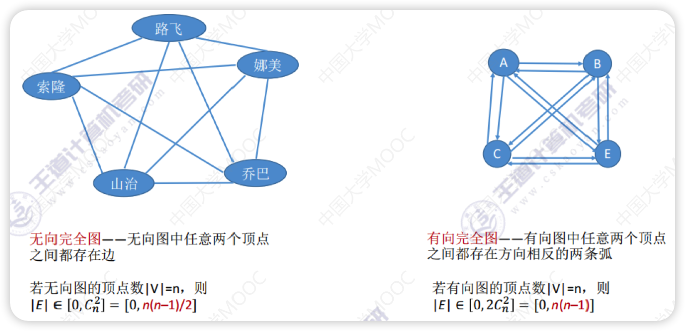
    • 任意两个顶点都存在边的图
    • 对于无向图，|E|的取值范围为0～n(n-1)/2，有n(n-1)/2条边的无向图称为无向完全图
    • 对于有向图，|E|的取值范围为0~n(n-1)，有n(n-1)条弧的有向图称为有向完全图

  1. 子图

    子图

    非子图

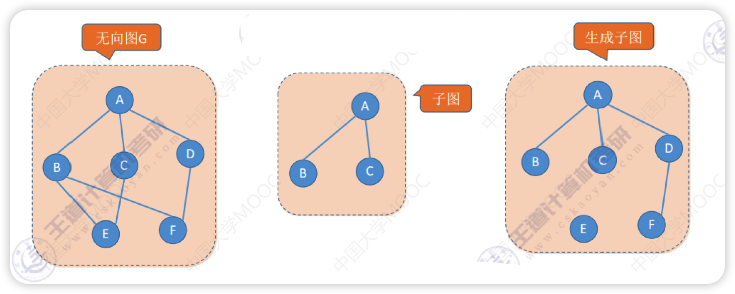
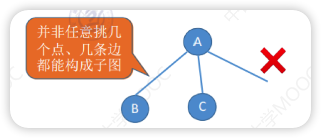
    • 子图就是原图扣掉几个顶点和顶点所在的边
    • 生成子图是只扣掉几条边的子图

  1. 顶点的度

    • 对于无向图：顶点 v 的度是指依附于该顶点的边的条数，记为 TD(v)

      • ycllo7

    • 对于有向图：

      • 入度是以顶点 v 为重点的有向边的数目，记为 ID(v)
      • 出度是以顶点 v 为起点的有向边的数目，记为 OD(v)
      • 顶点 v 的度等于入度与出度的和，记为 TD(v)=ID(v)+OD(v)
      • OJfnTP

  2. 顶点-顶点的关系描述

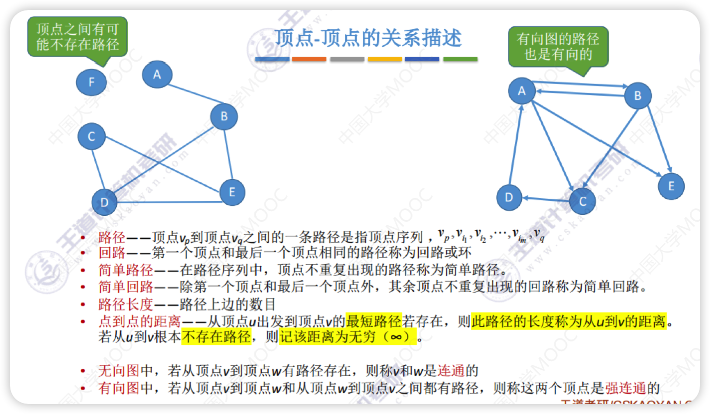
    bm3aqG

  1. 连通图

    连通图

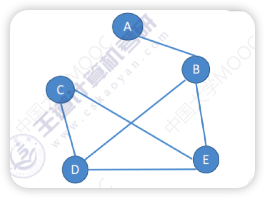
    👆连通图 👇非连通图

    非连通图

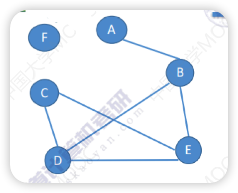
    如果无向图中任意两个顶点都能找到一条路连起来，那么这个无向图为连通图，否则就是非连通图

    • 对于 n 个顶点的无向图 G

      • 若 G 是连通图，则最少有 n-1 条边
      • 若 G 是非连通图，则最多有 C2n-1 条边

  2. 连通分量

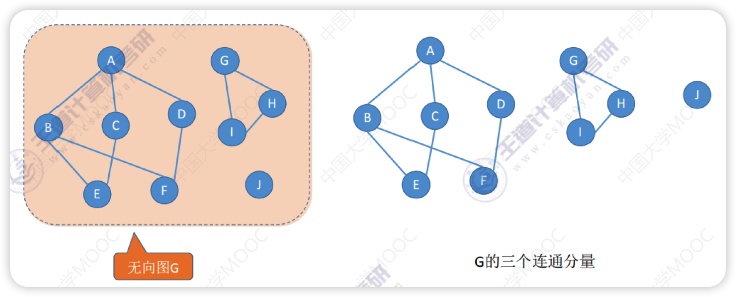
    8RinWu

    连通分量是指无向图中划分出来的连通图

    如上图 G 可以划分成三个连通子图，这三个连通子图就是 G 的连通分量

    • 一个无向图可以有多个连通分量

  3. 强连通图

    强连通图

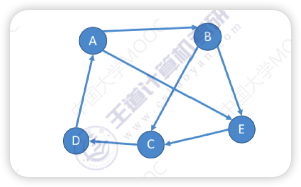
    有向图中任意两个顶点都有路径想通（正反向都通），则称这个图是强连通图

    • 对于 n 个顶点的有向图 G

      • 若 G 是强连通图，则最少有 n 跳边

  4. 强连通分量

    强连通分量

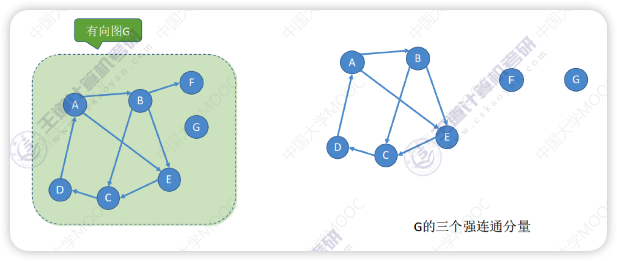
    与连通分量类似，子图必须强连通并且保留尽可能多的边

  1. 生成树

    生成树

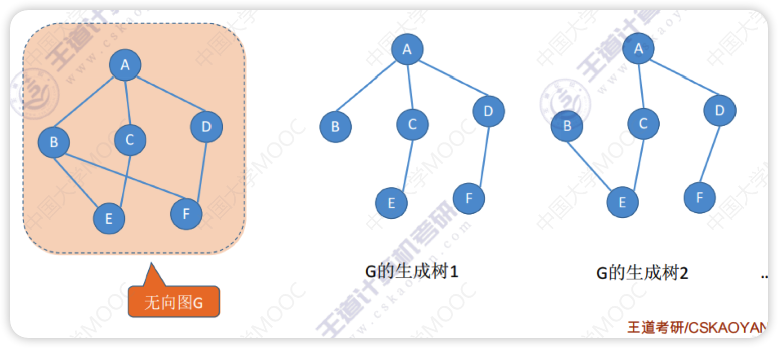
    连通图的生成树是包含图中全部顶点的一个极小连通子图

    即把连通图中的边在保证还是连通图的情况下尽可能多的去掉

    • n 个结点的连通图的生成树有n-1条边

  2. 生成森林

    生成森林

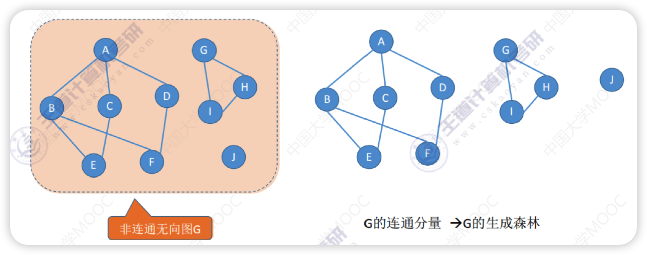
    类比生成树，将非连通图的每个连通分量的生成树放一块就构成了非连通图的生成森林

  1. 边的权

    在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值

  2. 带权图/网

    边上带有权值的图称为带权图，也称网

  3. 带权路径长度

    当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

  1. 有向树

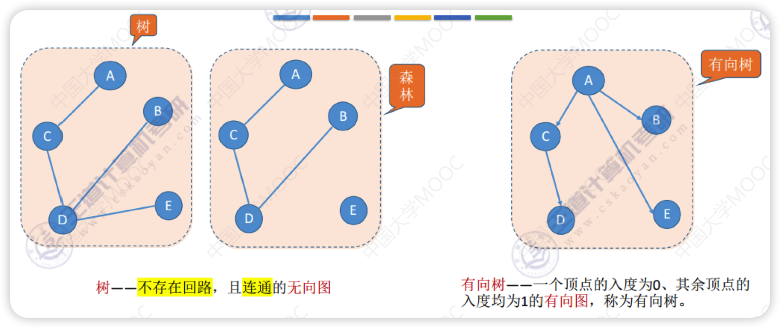
    4nLCQE

    长着树样的有向图

    • n 个顶点的树必须有 n-1 条边
    • n 个顶点的图，若 |E|>n-1，则一定有回路

错题集

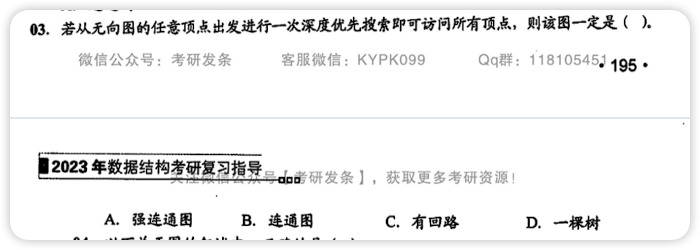
  1. 0dKDah

    答案与解析：
    答案：B
    解析：
    A选项不是无向图，直接pass
    B选项可以通过一次深度优先搜索访问到所有顶点
    C选项有回路但不一定连通，所以不能一次

  2. nxN1gc

    答案与解析：
    答案：B
    解析：
    n 个顶点的生成树具有 n-1 条边的极小连通子图
    n 个顶点的环有 n 条边，所以去掉任意一条边都有一个生成树
    也就是说可以有 n 棵生成树

  3. X6F8uF

    答案与解析：
    答案：C
    解析：
    I: 回路是路径，简单回路是简单路径
    II: 看6.2的邻接矩阵和邻接表就知道了
    III: 存在回路的图不存在拓扑序列

  4. ghXrfO

    答案与解析：
    答案：C
    解析：
    "任何情况下都是连通的"，"需要的变数最少是"表示6个顶点时是一个完全图，第7个顶点有一条边与完全图连接
    C26 + 1 = (6*(6-1))/2 + 1 = 16