二叉树的定义
二叉树就是最大度为 2 的有序树
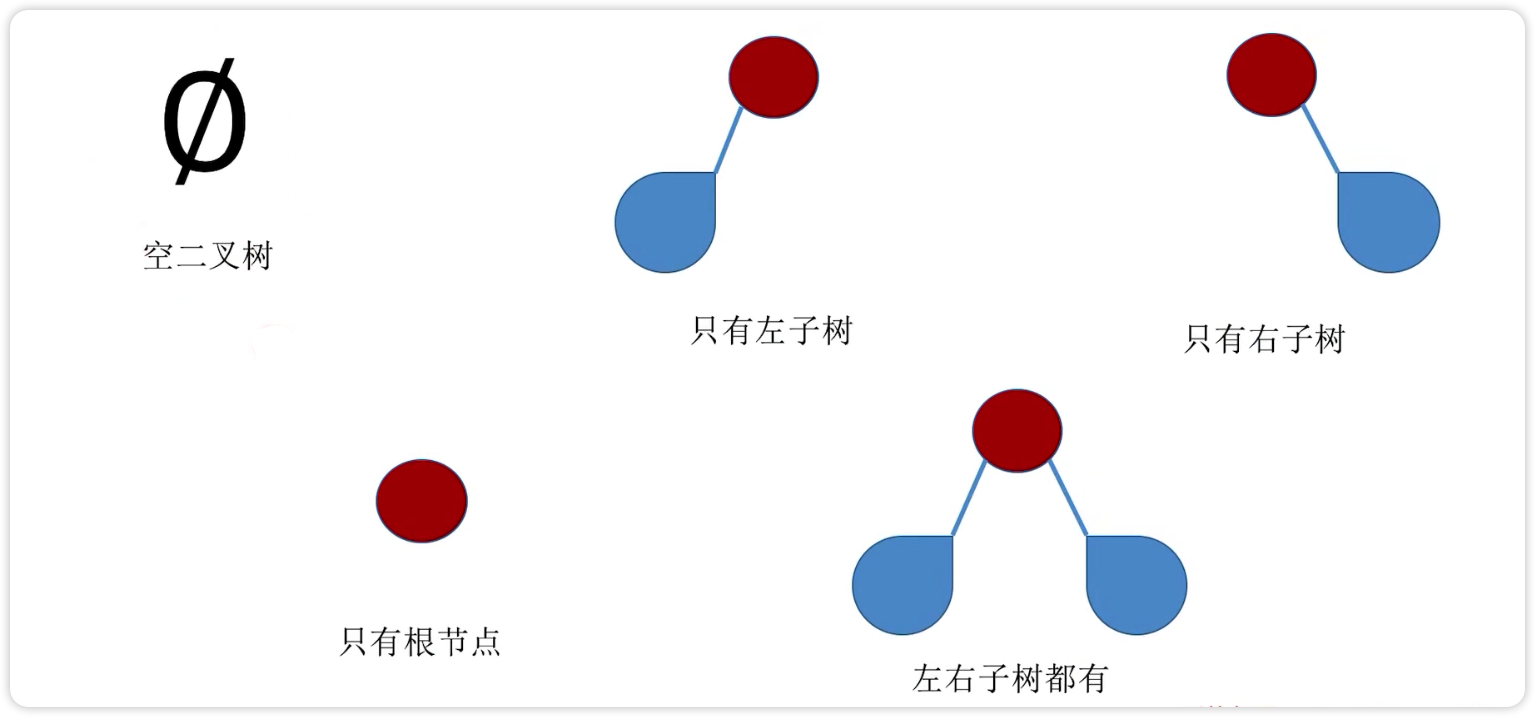
- 每个结点最多有两个子结点
- 左右子树不能颠倒
满二叉树
高度为 h,含有 2h-1 个结点
不存在度为 1 的结点
最后一层都是叶子结点,叶子结点都在最后一层
- 叶子结点个数为 2h-1
按层序 1 开始编号(下图这种)
- 结点 i 的左孩子为 2i
- 结点 i 的右孩子为 2i+1
- 结点 i 的父结点为 i/2(如果存在,小数向下取整)
完全二叉树
二叉树从左往右、从上往下一个个排,最后一层排满了就是满二叉树,没排满就是完全二叉树(如下图)
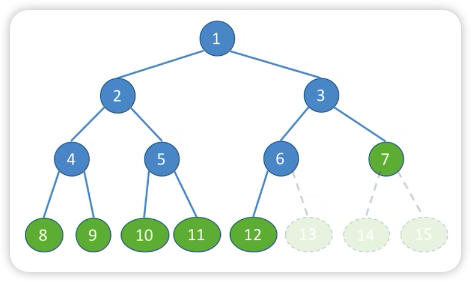 如果 14 或 15 号位置的结点存在,那也不是完全二叉树
如果没有 12 号结点但是有 13 号结点(指图上对应位置的结点),那也不是完全二叉树
如果 14 或 15 号位置的结点存在,那也不是完全二叉树
如果没有 12 号结点但是有 13 号结点(指图上对应位置的结点),那也不是完全二叉树
只有最后两层可能有叶子结点
最多只有一个度为 1 的结点
按层序 1 开始编号(这条与满二叉树一致)
- 结点 i 的左孩子为 2i
- 结点 i 的右孩子为 2i+1
- 结点 i 的父结点为 i/2(如果存在,小数向下取整)
如果一个完全二叉树有 n 个结点
- 如果 i<=(n/2) ,那么 i 结点为分支结点
- 如果 i>(n/2),那么 i 结点为叶子结点
二叉排序树(BST)
- 左子树上左右结点的关键字均小于根结点的关键字
- 右子树上左右结点的关键字均大于根结点的关键字
- 左子树和右子树又各是一棵二叉排序树
- 可以用宇元素的排序和搜索
平衡二叉树
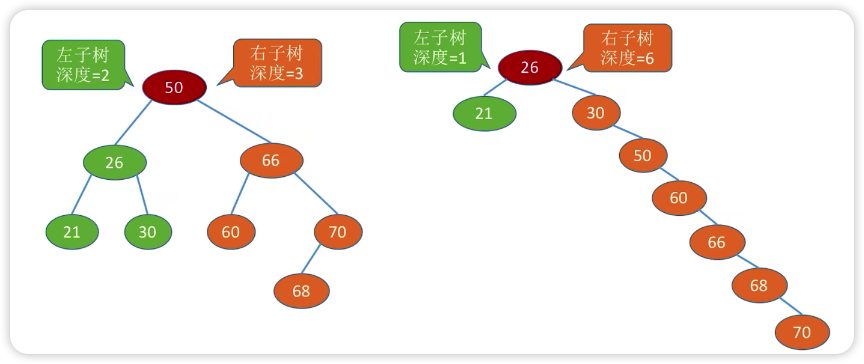
任何一个结点的左子树和右子树深度差不超过 1
下图左边为平衡二叉树,右边则不是
常考性质
二叉树
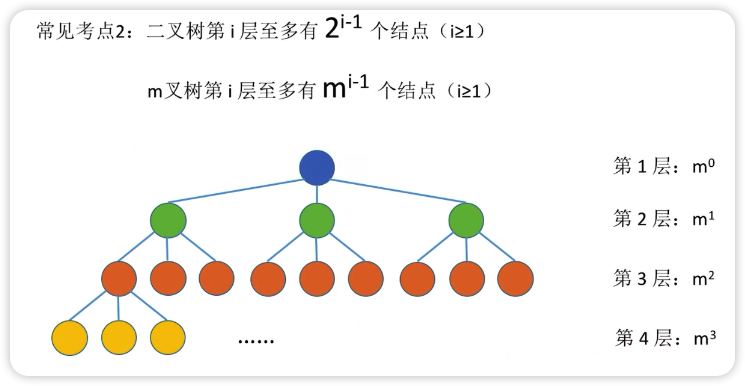
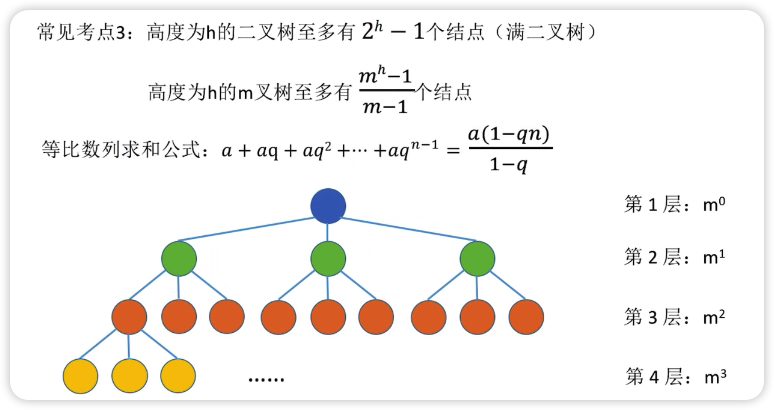 最少有 h 个结点
最少有 h 个结点
完全二叉树
具有 n 个结点的完全二叉树的高度 h=log2(n+1) (向上取整)或 h=1+log2n(向下取整)

第 i 个结点所在层次为 log2(n+1) 或 1+log2n
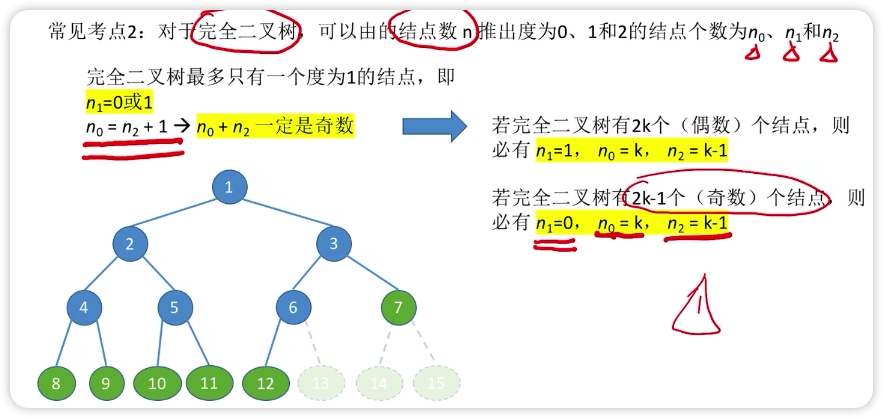
完全二叉树有 n 个结点
n 是偶数:
- n0=n/2
- n1=1
- n2=n/2-1
n 是奇数
- n0=(n+1)/2
- n1=0
- n2=(n+1)/2-1=(n-1)/2
错题集
答案与解析:
答案: C
解析:
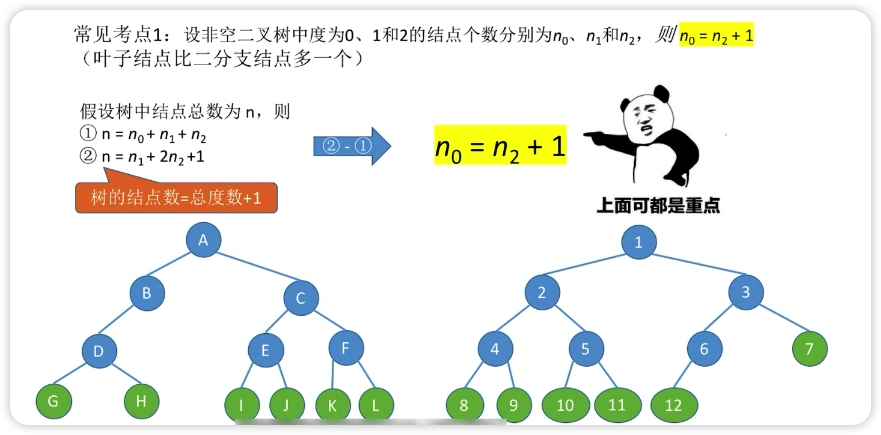
二叉树的总结点数=n1+2n2+1
即 2n=n1+2n2+1
显然 n1 不能是偶数,所以 C 错
答案与解析:
答案:D
解析:
先把叶子结点当成完全二叉树的叶子结点
叶子结点的个数 n0=116
所以总结点数 n=2n0=232
当然也可能是 231,最后结果都一样所以用 232 算就可以
此时 n1=1(231 的话这个值是 0)
剩下的结点都是只有一个结点,可以都当成只有左结点连在完全二叉树的根结点上边
剩下的结点的数量=2011-232=1779
所以没有右结点的数量=剩下的结点的数量+n0+n1=1779+116+1=1896
答案与解析:
答案:C
解析:
完全二叉树的叶子结点可能在最后一层或者倒数第二层
这里说结点个数最多,只有叶子结点在倒数第二层时符合
倒数第二层(第 6 层)的结点数 = 25=32
其中有 32-8=24 个结点有两个子结点(因为说了最多,所以不存在一个子结点的情况)
所以第 7 层结点的个数为 24x2=48 个
前 6 层(满二叉树)有 26-1=63 个结点
所以一共有 63+48=111 个结点
答案与解析:
答案:A
解析:
如果结点总数是 2k 的话就会存在一个 n1 结点,与题意不符
如果结点总数是奇数,与题意相符(没有子结点数为 1 的结点),总数为 2k-1



