KMP 算法

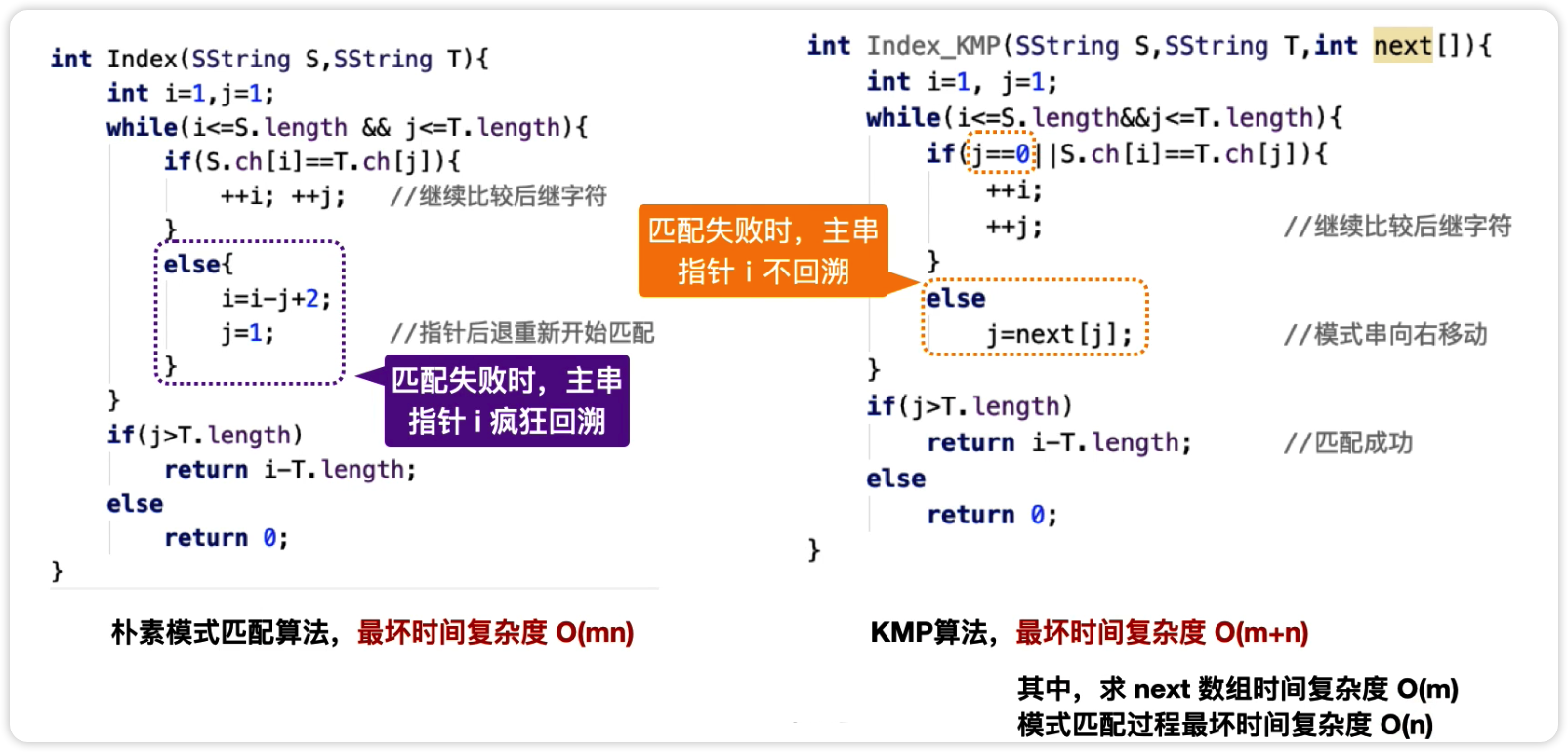
朴素模式匹配的缺点：当某些子串与模式串能部分匹配时，主串的扫描指针 1 经常回溯，导致时间开销增加，最坏时间复杂度 O(mn) KMP 算法：当子串和模式串不匹配时，主串指针 i 不回溯，模式串指针 j=next[j],算法平均时间复杂度 O(n+m) ，其中求 next 数组的时间复杂度为 O(m),模式匹配过程最坏时间复杂度为 O(n)

next[]

next[j]：在子串的第 j 个字符与主串发生失配时，则跳到子串的 next[j] 位置重新与主串当前位置进行比较

i 不变，j 变为 next[j],从 i 处重新开始匹配

手算 next 数组

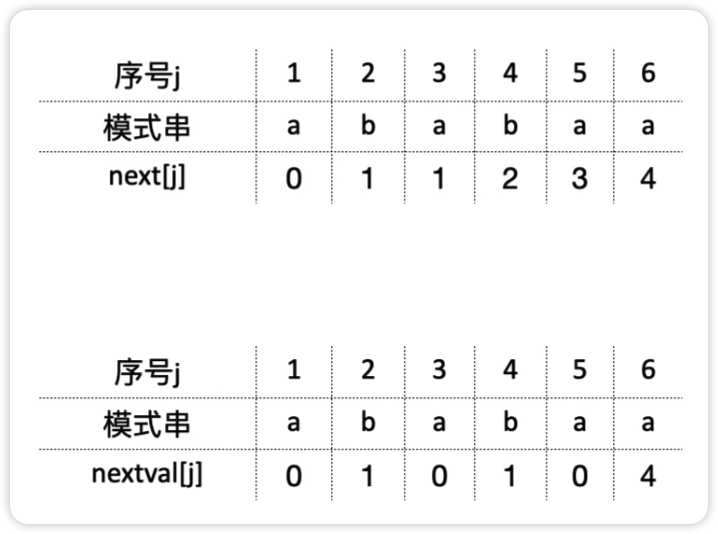
1. next 数组的长度与模式串 T 的长度相等，如模式串Google，此时 next 的最后一个元素为 next[6]

2. 任何模式串都一样，第一个字符不匹配时去找下一个子串，所以next[1]无脑写 0

3. 第 2 个子串不匹配的时候肯定都是去找第一个子串，所以next[2]无脑写 1

4. 第 3 个子串匹配时，在不匹配的位置前边（如下图）画一根分界线，模式串 T 一步步往后移动，如果分界线前的字符能对上或者过了分界线，把此时的 j 填入 next[3]

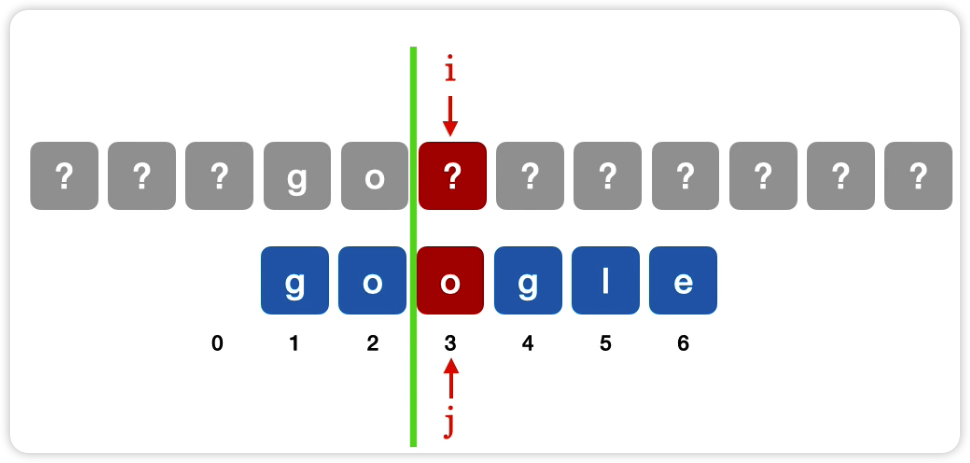
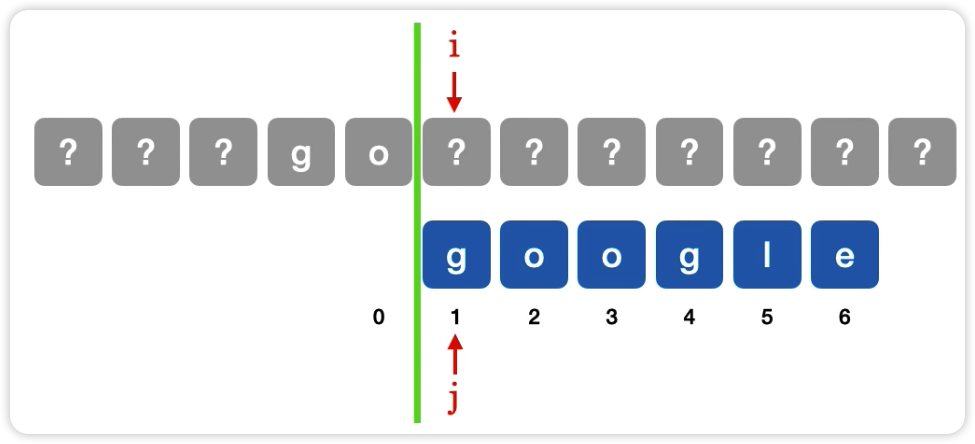
5. 同第 3 步，划线，移动，把 j 填入数组

6. 例：算'ababaaababaa'的next数组值

   1. 先把前两位无脑写01

      ababaaababaa

      ababaaababaa

      01

   2. 判断第三位，数组右移找到前面都一样或者空的情况，将对应的数字写到next中

      ababaaababaa

      ababaaababaa

      011

   3. 判断第四位，数组右移到前三位一样

      ababaaababaa

      ababaaababaa

      0112

   4. 判断第五位，数组右移到前四位一样

      ababaaababaa

      ababaaababaa

      01123

   5. 判断第六位，数组右移到前五位一样

      ababaaababaa

      ababaaababaa

      011234

   6. 判断第七位，数组右移到前六位一样

      ababaaababaa

      ababaaababaa

      0112342

   7. 判断第八位，数组右移到前七位一样

      ababaaababaa

      ababaaababaa

      01123422

   8. 判断第九位，数组右移到前八位一样

      ababaaababaa

      ababaaababaa

      011234223

   9. 判断第十位，数组右移到前九位一样

      ababaaababaa

      ababaaababaa

      0112342234

   10. 判断第十一位，数组右移到前十位一样

       ababaaababaa

       ababaaababaa

       01123422345

   11. 判断第十二位，数组右移到前十一位一样

       ababaaababaa

       ​ ababaaababaa

       011234223456

   12. 得出答案011234223456

KMP 优化

先求出next数组，再用next数组求nextval 如果nextval中某个字符的值等于他指向的next[j]的值，就直接把他的next[j]替换为他原本指向的值的next[j]