浮点数的表示

为什么要有浮点数

• 由于二进制表示小数会出现问题，如不能⽤⼆进制表示0.1，所以设计了浮点数来表示⼩数。
• 浮点数表示法能以适当的形式将⽐例因⼦表示再数据中，让⼩数点的位置根据需要⽽浮动。
• 在位数有限的情况下，既扩⼤了数的表示范围，⼜保持了数的有效精度

浮点数格式

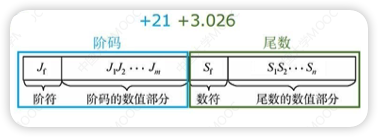
• 浮点数是指⽤符号，尾数，基数和指数来表示的⼩数

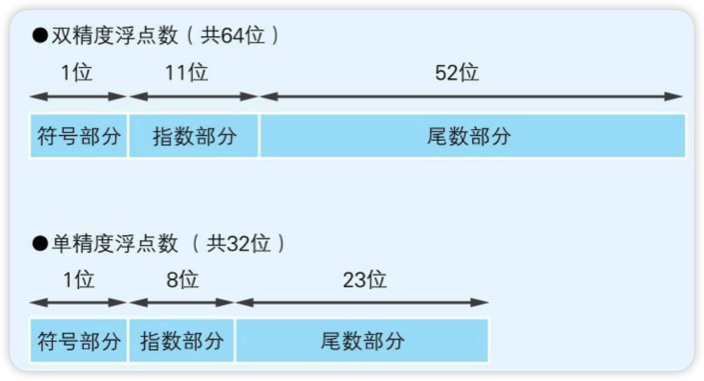
• 浮点数有两种：双精度浮点数double, 64位；单精度浮点数float, 32位

• 浮点数通常表示为$N=(-1{)}^S\times M\times R^E$$N=(-1)^S \times M \times R^E$

  • $(-1{)}^S$$(-1)^S$表示符号(±)，机器码中用1表示负，0表示正

  • $M$$M$表示尾数

    • 尾数的位数反映浮点数的精度
    • 使用正则表达式、将表现形式多样的浮点数统一为一种表达式
    • 规则：基数为2时，将⼩数点前⾯的值固定为1；基数为4时，尾数的最⾼两位不全为0

  • R表示基数

    • 二进制的基数为2
    • 基数越⼤，表示范围越⼤，但是精度越低

  • E表示指数(阶码)

    • 阶码的位数反映浮点数的表示范围

浮点数的表示范围

• 正上溢：大于最大正数

• 负上溢：小于绝对值最大负数

• 正下溢：0到最小正数之间

• 负下溢：0到绝对值最小负数之间

• 通俗来说，上溢就是大于最大数，下溢就是小于最小数

• a=001;1.1001;

  • 001对应真值为1，即阶码为1，尾数$1.1001$$1.1001$对应值$-\frac{7}{16}$$- \frac7{16}$
  • $a=2^1\times \frac{9}{32}=\frac{9}{16}$$a=2^1 \times \frac9{32}=\frac9{16}$

• b=001;0.01001

  • 001对应真值为1，即阶码为1，尾数$0.01001$$0.01001$对应值$+\frac{9}{32}$$+\frac9{32}$
  • $b=2^1\times \frac{9}{32}=\frac{9}{16}$$b=2^1 \times \frac9{32}=\frac9{16}$

浮点数尾数的规格化

• 规格化：规定尾数的最⾼数位必须是⼀个有效值(1)

• 采用规格化浮点数的目的是为了增加数据的表示精度

• 左归：当浮点数运算的结果为非规格化时要进行规格化处理,将尾数算术左移一位,阶码减1。

• 右归：当浮点数运算的结果尾数出现溢出(双符号位为01或10)时,将尾数算术右移一位,阶码加1。

• 原码表示的尾数规格化，尾数的最高数值位必须是1

• 补码表示的尾数规格化，尾数的最高数值位必须和尾数符号位相反

  

  

IEEE 754浮点数的范围[🌟🌟🌟常考选择]

尾数用原码表示，阶码用移码表示(移码符号位与补码相反)

• 单精度

  • 最小值：E=1，M=0，$1.0\times 2^{1-127}=2^{-126}$$1.0\times 2^{1-127}=2^{-126}$
  • 最大值：E=254，M=.111...，$1.1....1\times 2^{254-127}=2^{127}\times (2-2^{-23})$$1.1....1 \times 2^{254-127} = 2^{127} \times (2 - 2^{-23})$
  • 单精度阶码取值1～254，偏移值为127，最小值为$1\times 2^{1-127}$$1 \times 2^{1-127}$，最大值为$(2-2^{23})\times 2^{234-127}$$(2-2^{23}) \times 2^{234-127}$

• 双精度

  • 最小值：E=1，M=0，$1.0\times 2^{1-1023}=2^{-1022}$$1.0 \times 2^{1-1023} = 2^{-1022}$
  • 最大值：E=2046，M=.111...，$1.1....1\times 2^{2046-1023}=2^{1023}\times (2-2^{-52})$$1.1....1 \times 2^{2046-1023} = 2^{1023} \times (2 - 2^{-52})$
  • 双精度阶码取值1～2046，偏移值为1023

• 规定除去E为全0和全1表示0和无穷大的情况，所有阶码范围为1～254

浮点数的加减运算

• 对阶

  • ⽬的：使两个操作数的⼩数点位置对⻬
  • 对阶操作是把较⼩的阶码调整到较⼤的阶码
  • 阶码增⼤，尾数右移
  • ⽆阶码减⼩的情况

• 尾数求和

  • 对尾数进行加减法

• 规格化

  • 规格化浮点数

• 舍入

  • 舍入是浮点数概念，定点数无舍入
  • 浮点数舍入的情况：对阶或者右规格化
  • 舍入不一定产生误差(后几位为0时不产生误差)
  • 0舍1入

• 溢出判断

  • 如果双符号位为01或10时，溢出

• 选择题可以直接用数学知识计算

C语言中的浮点数

• 以下转换的范围和精度都从小到大，转换过程没有损失

  • char --> int --> long --> double
  • float -->double

• int/float --> double (能保留精确值)

• int --> float (不会发生溢出，int过大可能会发生舍入)

• double --> float (可能会发生溢出和舍入)

• float/double --> int (可能会发生溢出和舍入)

定点数与浮点数的区别

错题集

1. 

   答案与解析：

   
   答案： C
   解析：
   尾数为补码表示，且为1.0xxx或者0.1xxx时为规格化数据，所以需要左移一位，同时阶码-1

2. 

   答案与解析：

   
   答案： B
   解析：
   原码表示时，正数的规格化形式为0.1xxx，负数为1.1xxx

3. 

   答案与解析：

   
   答案： C
   解析：
   对接操作中，只有小阶调整到与大阶一致，不存在阶码减小的情况，AB错误

4. 

   答案与解析：

   
   答案： D
   解析：
   

5. 

   答案与解析：

   
   答案： A
   解析：
   (f1) = 1100 1100 1001 0000 ... 0000
   (f2) = 1011 0000 1100 0000 ... 0000
   显然第一位都是1，符号相同，都是负数
   f1 = -(1.001)₂ * 2²⁶
   f2 = -(1.1)₂ * 2^-30
   显然f1绝对值更大，即x < y

6. 

   答案与解析：

   
   答案： D
   解析：
   I: 对阶是阶码小的变成与阶码大的一致，阶码大的都没溢出，所以肯定不会引起溢出
   II: 右规和尾数舍入过程，阶码+1可能引起阶码上溢
   III: 同II
   IV: 尾数溢出可能只产生误差，不一定溢出

7. 

   答案与解析：

   
   答案： A
   解析：
   C800 0000H = 1100 1000 000 ... 0000
   1. 如果是float型：-1.0*2¹⁷
   2. 如果是int型：原码为1011 1000 ... 0000 = -7*2²⁷