基本运算部件

“我不知道你们的名字，”冯·诺伊曼拍拍前两个士兵的肩，“你们两个负责信号输入，就叫‘入1’、‘入2’吧，”他又指指最后一名士兵，“你，负责信号输出，就叫‘出’吧。”他伸手拨动三名士兵，“这样，站成一个三角形，出是顶端，入1和入2是底边。”[...]冯·诺伊曼接过来分给三名士兵，每人一白一黑，说：“白色代表０，黑色代表1。好，现在听我说，出，你转身看着入1和入2，如果他们都举黑旗，你就举黑旗，其他的情况你都举白旗，这种情况有三种：入1白，入2黑；入1黑，入2白；入1、入2都是白。”[...]“这三个人组成了一个计算系统的部件，是门部件的一种，叫‘与门’。”冯·诺伊曼说完停了一会儿，好让皇帝理解。”

摘录来自 《三体》刘慈欣

• 逻辑运算符

  • 与(·)(&&)

    • 两个都为1时结果为1

  • 或(+)(||)

    • 两个有一个为1时结果为1

  • 非(Ᾱ,表达式上边加个横线)(!)

    • 取反

  • 异或(⊕)

    • 两个不同时取1

  • 表达式(这里的乘和加是与和或)

    • $\overline{A+B}=\overline{A}\cdot \overline{B}$$\overline{A+B} = \bar A \cdot \bar B$（离散数学德摩根率)
    • $\overline{A\cdot B}=\overline{A}+\overline{B}$$\overline{A \cdot B} = \bar A + \bar B$
    • $A(C+D)=A\cdot C+A\cdot D$$A(C+D) = A \cdot C + A \cdot D$
    • $ABC=A(BC)$$ABC = A(BC)$
    • $A+B+C=A+(B+C)$$A+B+C=A+(B+C)$

一位全加器（FA）

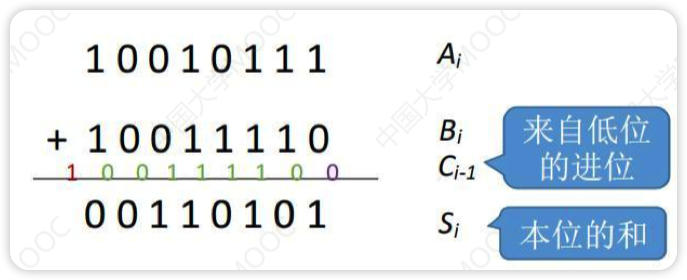
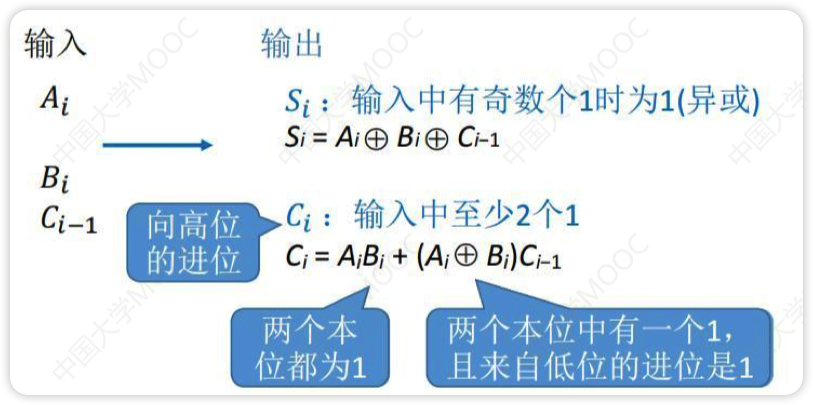
A_i+B_i如果两个数相同，加一块后一定是0(先不考虑进位)，否则一定是1，所以可以直接用异或门进行计算

因为可能有前面的进位C_i-1，所以计算一次后需要与低位的进位再通过一次异或门，这样就能求出S_i

只有A_i与B_i同时为1时需要进位，也可能是A_i+B_i第一次通过异或门后得到的数与C_i-1同时为1时需要进位，不管哪个符合都需要进位

所以A_i和B_i通过一次与门，A_i+B_i第一次通过异或门后得到的数和C_i-1通过一次与门，然后这两个结果通过一次或门就可以得到C_i

这样就可以得到一个电路图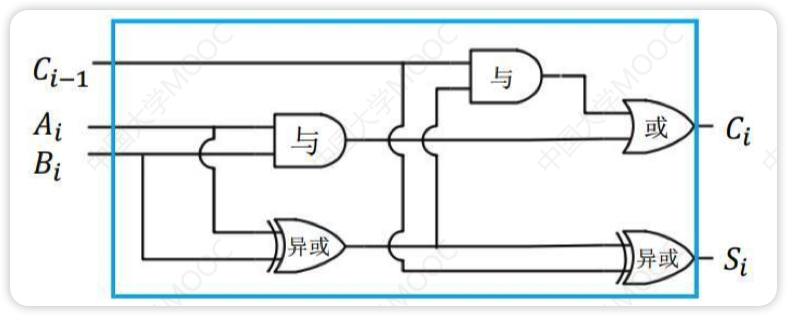

对蓝色框部分进行封装就可以变为一位全加器（full adder,简称FA）

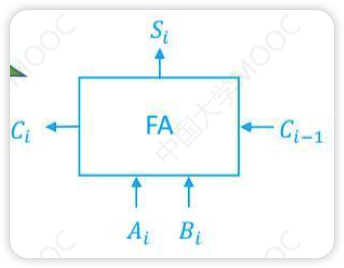
• FA是最基本的加法单元
• input: 加数A_i和B_i，还有低位传进来的C_i-1,默认为0
• output: 本位和S_i，还有向高位的进位C_i
• 和表达式: $S_i=A_i\oplus B_i\oplus C_{i-1}$$S_i = A_i \oplus B_i \oplus C_{i-1}$
• 进位表达式: $C_i=A_i{B}_i+(A_i\oplus B_i)C_{i-1}$$C_i = A_iB_i + (A_i \oplus B_i)C_{i-1}$

串行加法器

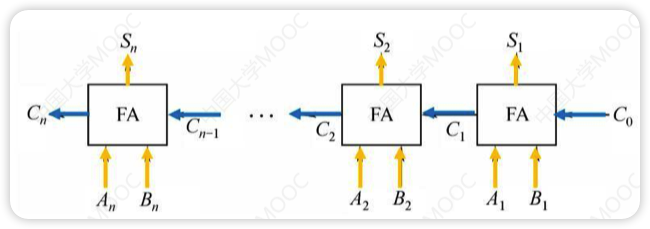
• 把n个FA串连起来，这样就能得到n位加法器
• 每一级进位直接依赖于前一级的进位，进位信号是逐级形成的
• 最长运算时间主要由进位信号的传递时间决定

并行加法器

心平气和，学不会就摆烂，也不是什么重点

根据FA的表达式，如果计算两位数相加

$G_i=A_i{B}_i,P_i=A_i\oplus B_i$$G_i = A_iB_i,P_i=A_i \oplus B_i$

$C_1=G_1+P_1{C}_0$$C_1 = G_1+P_1C_0$

$C_2=G_2+P_2{C}_1=G_2+P_2(G_1+P_1{C}_0)=G_2+P_2{G}_1+P_2{P}_1{C}_0$$C_2 = G_2 + P_2C_1 = G_2 + P_2(G_1 + P_1C_0)=G_2+P_2G_1+P_2P_1C_0$

$C_3=G_3+P_3{G}_2+P_3{P}_2{G}_1+P_3{P}_2{P}_1{C}_0$$C_3 =G_3+P_3G_2+P_3P_2G_1+P_3P_2P_1C_0$

$C_4=G_4+P_4{G}_3+P_4{P}_3{G}_2+P_4{P}_3{P}_2{G}_1+P_4{P}_3{P}_2{P}_1{C}_0$$C_4 =G_4+P_4G_3+P_4P_3G_2+P_4P_3P_2G_1+P_4P_3P_2P_1C_0$

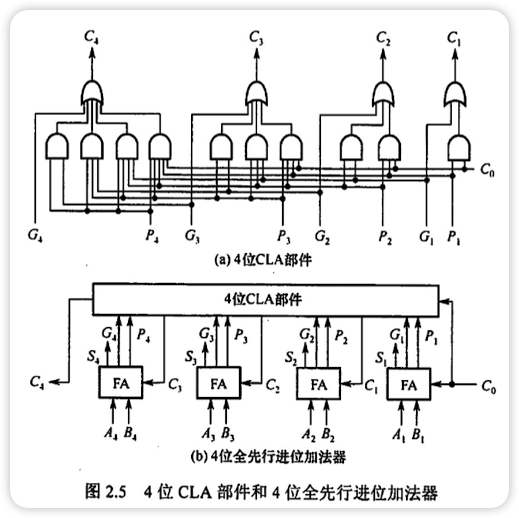
• CLA(超前进位部件)是实现上述表达式的部件
• 这种进位方式快速，与位数无关，当位数多时采用全先行进位是不现实的
• 采用并行进位的目的是：提高加法器运算速度
• 通常采用两级或多级先行进位加法器

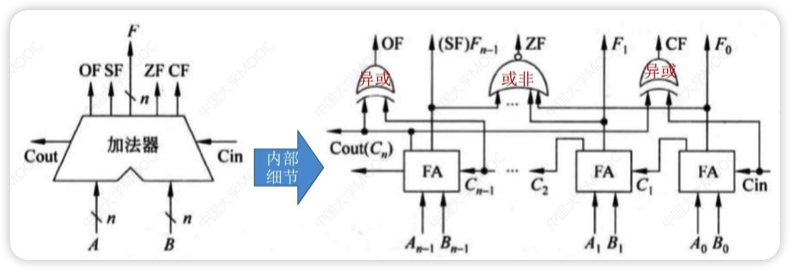
带标志加法器

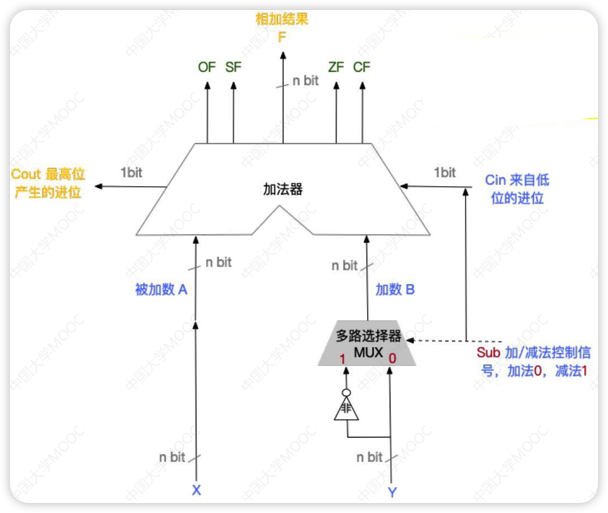
• 不仅能计算和/差，还能生成相应的标志信息

• 为了加快加法运算速度，实际电路一定使用多级先行进位方式

• OF(Overflow Flag): 溢出标志，溢出时为1，否则为0

  • 硬件计算方法: $OF=\text{最}\text{高}\text{位}\text{产}\text{生}\text{的}\text{进}\text{位}\oplus \text{次}\text{高}\text{产}\text{生}\text{的}\text{进}\text{位}=Cout\oplus C_{n-1}$$OF=最高位产生的进位 \oplus 次高产生的进位=Cout \oplus C_{n-1}$
  • OF位对无符号数的加减法无意义

• SF(Sign Flag): 符号标志，结果为负数时为1，否则为0

  • 硬件计算方法: $SF=\text{最}\text{高}\text{位}\text{的}\text{本}\text{位}\text{和}=F_{n-1}$$SF = 最高位的本位和=F_{n-1}$
  • SF位对无符号数的加减法无意义

• ZF(Zero Flag): 零标志，结果为0时为1，否则为0

  • 硬件计算方法: 两个数的运算结果为n bit，只有n bit全为0时，ZF=1

• CF(Carry Flag): 进位/借位标志，进位/借位时为1，否则为0

  • 硬件计算方法: $\begin{array}{c}CF=\text{最}\text{高}\text{位}\text{产}\text{生}\text{的}\text{进}\text{位}\oplus sub\{\begin{array}{ll}sub=1,& \text{表}\text{示}\text{减}\text{法}\\ sub=0,& \text{表}\text{示}\text{加}\text{法}\end{array}=Cout\oplus Cin\end{array}$$CF = 最高位产生的进位 \oplus sub\left \{\begin{array}{l} sub=1, &表示减法 \\ sub=0, &表示加法 \end{array}\right. = Cout \oplus Cin$
  • C_in=0时CF=C_out;C_in=1时CF=!C_out(取反)
  • CF位对符号数的加减法无意义

• A-B<0时，CF=1；溢出时OF=1

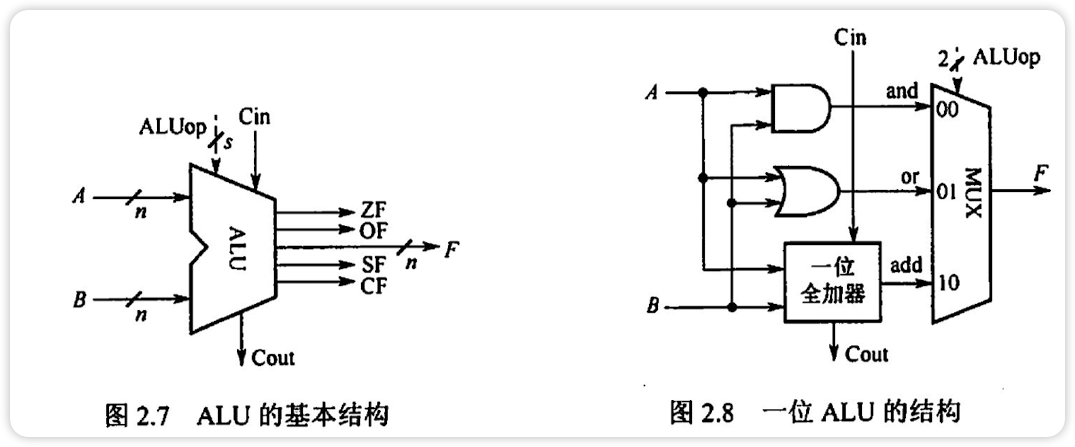
算术逻辑单元（ALU）

• ALU的核心是带标志加法器
• ALU是功能强大的组合逻辑电路，能进行算术运算，逻辑运算，移位操作
• ALUop是操作控制端，决定ALU所执行的处理操作
• ALUop的位数决定了操作的种类，位数为3时，有$2^3=8$$2^3=8$种操作
• 在ALUop的控制下，由一个多路选择器MUX选择输出某种操作结果
• MUX是多路选择开关，它从多个输入信号中选择一个送到输出端

定点数的运算

• 定点数是位数不变的数
• 可以不用考虑小数还是整数

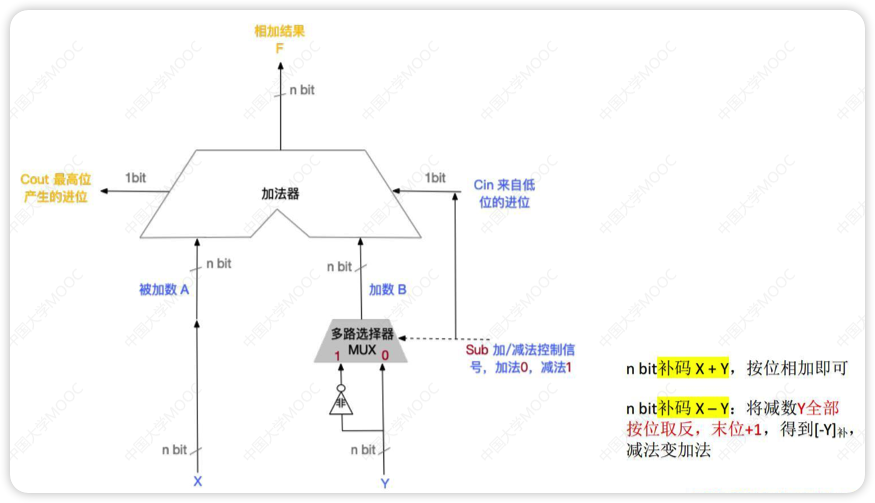
加减法[常考]

补码加减法运算

• 按二进制运算规则计算
• 符号位参与运算
• 高位丢弃

溢出判别方式[🌟🌟🌟]

• 仅当两符号相同的数相加或两个符号相异(其实还是同符号相加)的数相减才可能产生溢出

• 一般用异或门来实现溢出判断电路

• 计算时，左边出现溢出，将溢出位丢掉

• 判断溢出的方式

  • 采用一位符号法

    • 参与操作的两个数符号相同，结果又与原操作数符号不同，则溢出

  • 采用一位符号位根据数据位的判断情况判断溢出

    • 若符号位的进位和最高数位的进位相同，则没有溢出

  • 双符号法/模4补码

    • 模4补码有模2补码的所有优点，且更容易检查溢出问题

    • 模4补码存储时只需要一个符号位

    • 模4补码计算时(在ALU中)需要两个符号位

    • 最高位代表真正的符号，低位符号参与移位操作

    • 两个符号的意义

      • 00: 正数，无溢出
      • 01: 正溢出
      • 10: 负溢出
      • 11: 负数，无溢出

移位计算

算术移位

• 算术移位的对象是有符号数，移位过程中符号位保持不变

• 原码的算数移位：符号位保持不变，数值位进行移位

  • 右移：高位补0，低位舍弃。如果舍弃的低位=0，相当于➗2，否则会丢失精度

    丢失精度

    3的原码00000011，右移后变成00000001=1
    3/2=1.5，所以丢失了0.5，即丢失精度

  • 左移：低位补0，高位舍弃。如果舍弃的高位=0，相当于✖️2，否则会出现严重误差

    严重误差

    -80=11010000,左移后变成10100000=-32
    -80*2=-160,与-32完全不同，即出现严重误差

• 反码的算数移位

  • 正数原反补相同所以参考原码
  • 负数右移：高位补1，低位舍弃
  • 负数左移：低位补1，高位舍弃

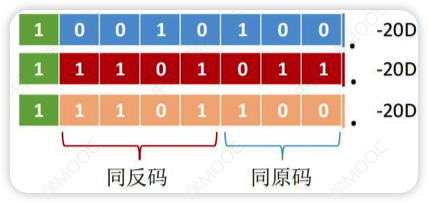
• 补码的算数移位

  • 正数原反补相同所以参考原码

  • 负数右移：高位补1，低位舍弃(同反码)

  • 负数左移：低位补0，高位舍弃(同原码)

  • 规律：负数补码中，最右边的1及其右边同原码，左边同反码

    

逻辑移位

当作无符号数的算数移位

• 左移低位补0
• 右移高位补0

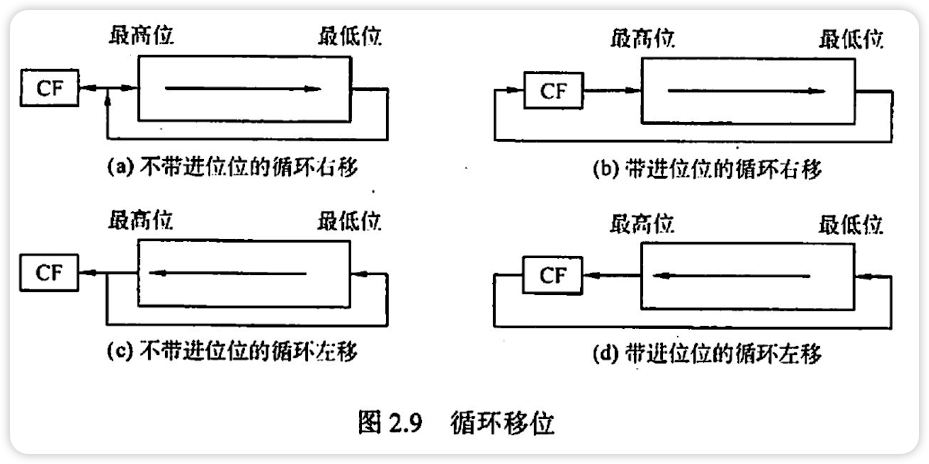
循环移位

• 不带进位位：用移出的位补上空缺（传送带）
• 带进位位：移出的位放到进位位，进位位补上空缺（传送带多了一节）

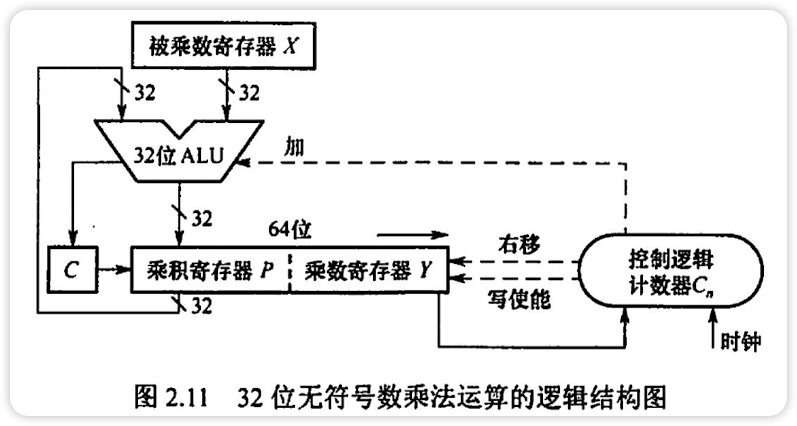
乘法[易考概念]

乘法运算由累加和右移操作实现

原码一位乘法

• 符号位和数值位是分开求的
• 符号位不参与运算，同号为正，异号为负
• 乘积符号 = 两个数的符号位的异或
• 乘积数值 = 两个数的绝对值相乘的结果
• 积和被乘数采用双符号位
• 最多进行n次加法运算，n次移位

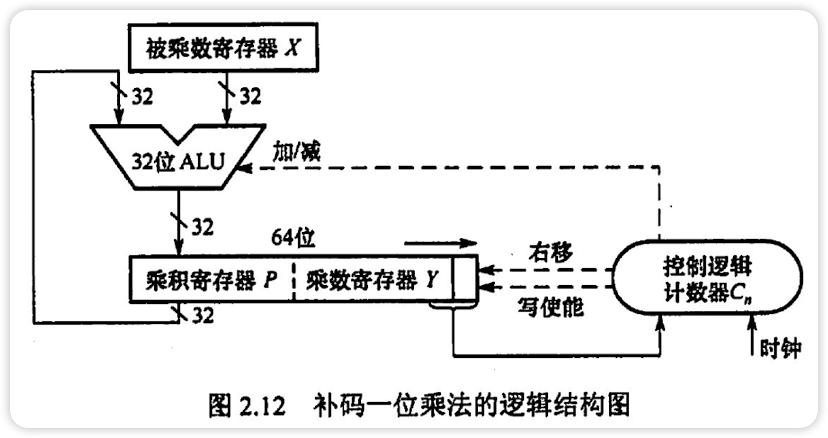
补码一位乘法[Booth算法]

• 是一种有符号数的乘法

• 最多进行n次移位，n+1次加法运算

• Booth算法的移位规则

  yn(高位)	yn+1(低位)	操作
  0	0	部分积右移一位
  0	1	部分积加[X]补,右移一位
  1	0	部分积加[-X]补,右移一位
  1	1	部分积右移一位

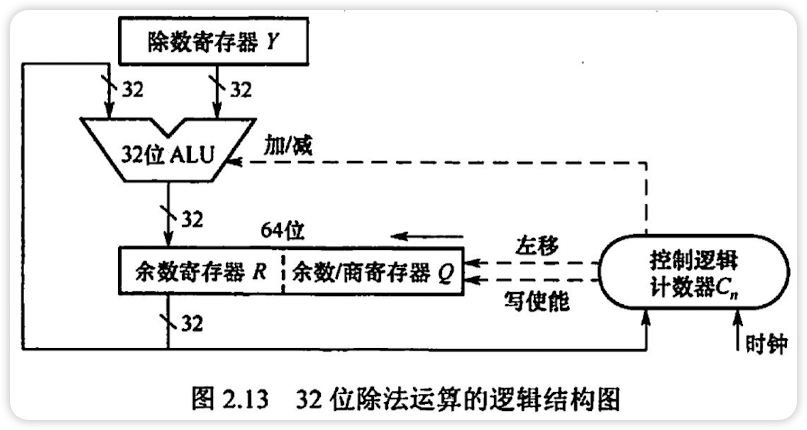
除法

除法运算由累加和(逻辑)左移实现

原码除法运算[不恢复余数法]

• 符号扩展

  • 正数符号位不变，扩展位填充0

  • 负数原码表示和正数相同，符号位为1

  • 负数补码符号位不变，附加位用1(整数)或0(小数)进行填充

    • 如16位补码Ox8FA0扩展为32位为OxFFFF 8FA0
    • 如-64位的补码是1100 0000,则其十六进制为OxFFFF FFC0

• 该方法商符和商值分开进行

• 商符由两个操作数的符号位异或形成

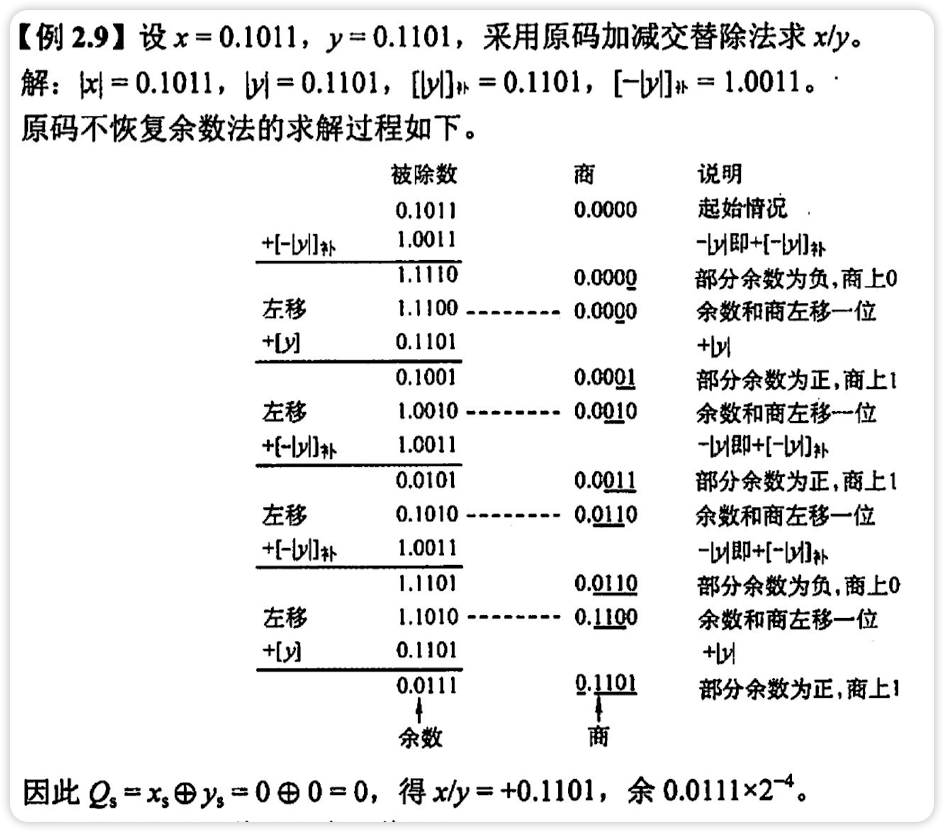
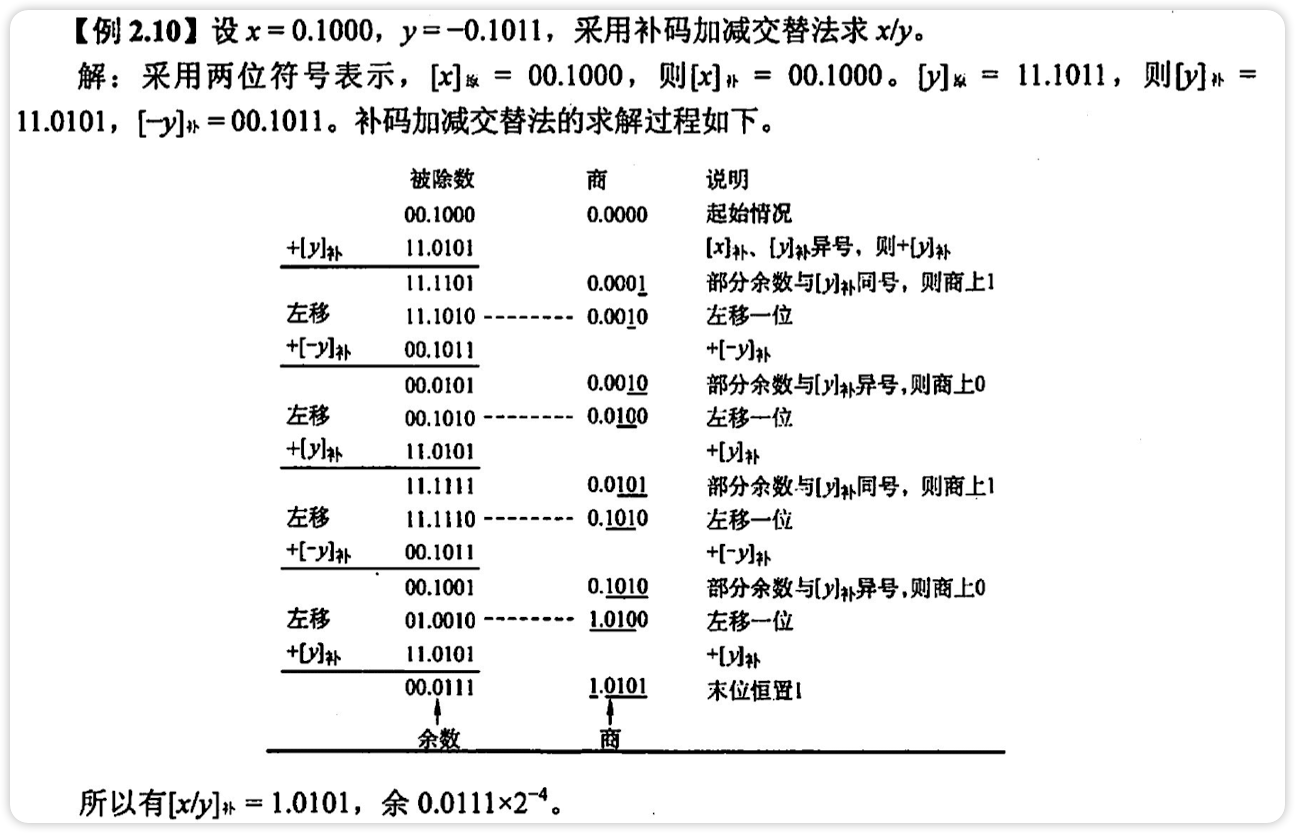
补码除法运算[加减交替法]

• 该方法符号位和数值位一起参加运算，商符自然形成

  1. 根据被除数和除数的符号决定做加法还是减法

  2. 上商的原则根据余数和除数的符号位共同决定

     • 同号上商1
     • 异号上商0

  3. 最后一步商置1

C语言中的整数类型及类型转换[🌟🌟🌟]

有符号数和无符号数的转换

• 强制类型转换的结果保持位置不变，改变了解释这些位的方式

xxxxxxxxxx
20
1
int main() {
2
    //例1
3
    // x的补码为          1110 1111 0001 1111
4
    short x1 = -4321;
5
    // 无符号位y的二进制为 1110 1111 0001 1111  真值61215
6
    unsigned short y1 = (unsigned short) x1;
7
    printf("x1=%d\ny1=%u\n\n", x1, y1);// %u是按unsigned int输出
8
    // x1=-4321
9
    // y1=61215
10

11
    //例2
12
    // x2               1111 1111 1111 1111
13
    unsigned short x2 = 65535;
14
    // y2               1111 1111 1111 1111  真值-1
15
    short y2 = (short) x2;
16
    printf("x2=%u\ny2=%d", x2, y2);
17
    // x2=65535
18
    // y2=-1
19
    return 0;
20
}

不同字长正数之间的转换

• 当大字长变量向小字长变量强制类型转换时

  • 系统把多余的高位部分直接截断，低位直接赋值

• 短字长整数到长字长整数的转换时

  • 要使相应的位值相等，也要对高位部分进行填充
  • 原数位无符号整数，填充0
  • 原数位为有符号整数，进行符号填充

• char为8位无符号整数，转换为int时高位补0即可

xxxxxxxxxx
25
1
int main(){
2
    //例1
3
    // int 占用32位(4B)
4
    //x: 0x000286a1
5
    //u: 0xffff7751
6
    int x = 165537, u = -34991;
7
    //y: 0x86a1
8
    //v: 0x7751
9
    short y = (short) x, v = (short) u;
10
    printf("x=%d, y=%d\n", x, y);//x=165537,y=-31071
11
    printf("u=%d, v=%d\n", u, v);//u=-34991,v=30545
12

13
    //例2
14
    //x1: 0xef1f
15
    //y1: 0xffffef1f
16
    short x1 = -4321;
17
    int y1 = x1;
18
    //u1: 0xef1f
19
    //v1: 0x0000ef1f
20
    unsigned short u1 = (unsigned short)x1;
21
    unsigned int v1 = u1;
22
    printf("x=%d, y=%d\n", x1, y1);//x=-4321, y=-4321
23
    printf("u=%d, v=%d\n", u1, v1);//u=61215, v=61215
24
    return 0;
25
}

数据的存储和排列[🌟🌟🌟]

数据的大端方式和小端方式存储

• 用最低有效字节LSB和最高有效字节MSB分别表示数的低位和高位
• short占2字节=16位
• int、float占4字节=32位
• double占8字节=64位
• 大端方式：按MSB到LSB顺序存储数据（正常人看的顺序）
• 小端方式：按LSB到MSB顺序存储数据（反过来的顺序） - 假设i的地址为0800H,i的机器数为01234567H - 则地址0800H表示的内容为67H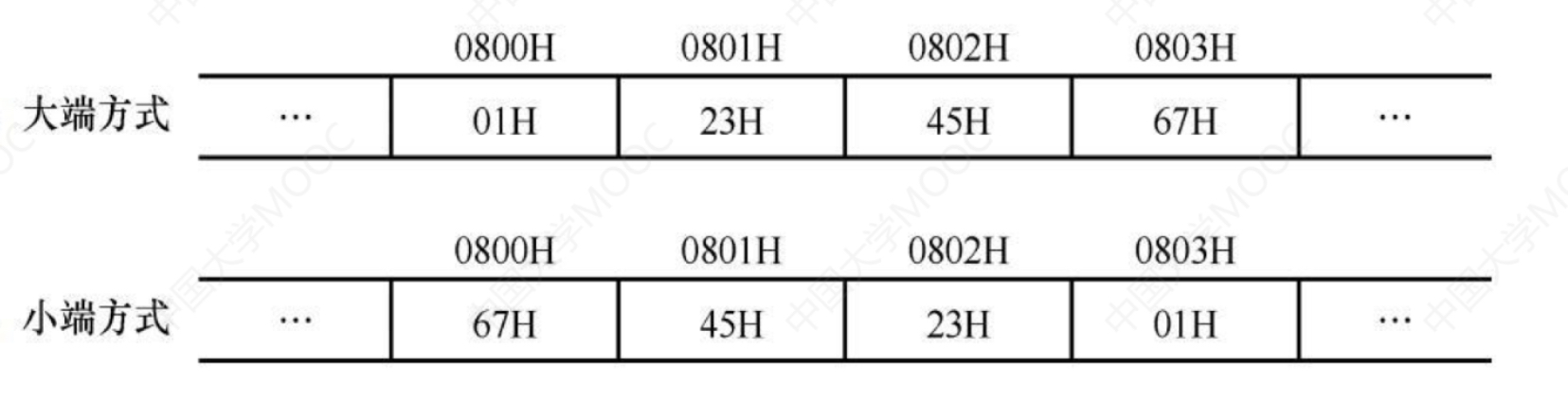

数据按边界对齐方式存储

• 边界对齐相对于边界不对齐是一种空间换时间的思想(摆整齐一点方便找)
• 存储字长为32位时，半字是2的整数倍，字地址是4的整数倍，字节大小为8位
• 边界对齐虽然浪费了一些存储空间，但是可以提高取指令和取数的速度
• 边界不对齐可以充分利用存储空间，但是效率较低
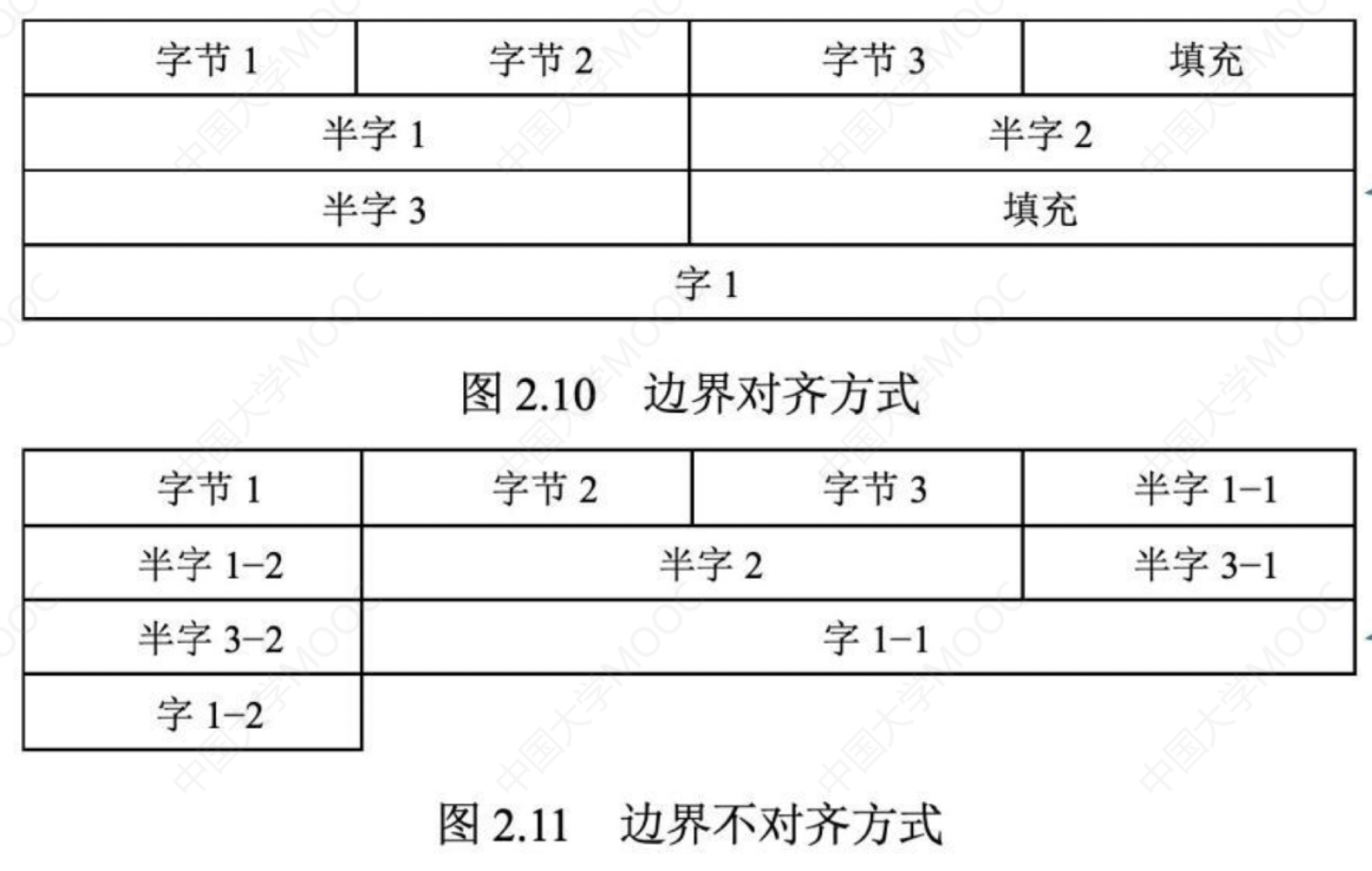
• char 偏移量为sizeof(char) 即 1 的倍数
• short 偏移量为sizeof(short) 即 2 的倍数
• int 偏移量为sizeof(int) 即 4 的倍数
• float 偏移量为sizeof(float) 即 4 的倍数
• double 偏移量为sizeof(double) 即 8 的倍数

例1:

25
1
struct asd1{
2
    char a;
3
    int b;
4
    short c;
5
};//12字节
6
 
7
struct asd2{
8
    char a;
9
    short b;
10
    int c;
11
};//8字节
12

13
struct asd3{
14
    char a;
15
    char b;
16
    short c;
17
    int d;
18
};//8字节
19
 
20
struct asd4{
21
    char a;
22
    short b;
23
    char c
24
    int d;
25
};//12字节

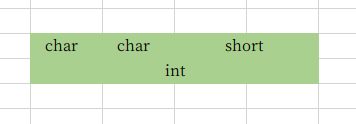
C语言结构体中不同的声明顺序导致结构体占用的空间也不一样

• 数据类型自身的对齐值：对于 char 型数据，其自身对齐值为1，对于 short 型为2，对于 int，float，double 类型，其自身对齐值为 4，单位字节。(上面的例子)

• 结构体或者类的自身对齐值：其成员中自身对齐值最大的那个值。

• 数据成员、结构体和类的有效对齐值：自身对齐值和指定对齐值中小的那个值。

错题集

1. 

   答案与解析：

   
   答案： D
   解析：
   溢出标志即为状态寄存器，A正确
   数据总线供ALU与外界交互数据使用，B正确
   ALU为运算器核心，C正确
   地址寄存器不属于运算器，D错误

2. 

   答案与解析：

   
   答案： C
   解析：
   不带进位位的循环左移将最高位进入最低位和标志寄存器C位
   不带进位位的循环位移=传送带

3. 

   答案与解析：

   
   答案： B
   解析：
   扩展为高位需要补符号位（正数补0，负数补1）
   16位补码第一位是8，换成2进制就是1000，也就是负数，所以扩展后前面为FFFF，排除A和D
   C选项后面的FFA0和题目不一样，所以选B（拓展了不会改变原数值）

4. 

   答案与解析：

   
   答案： B
   解析：
   A:模4运算更容易检查加减运算中的溢出问题
   B、C、D:任何一个正确的数值，模4补码的两个符号位总是相同的，所以只需要存储一个符号位；只有把两个模4补码的数送往ALU完成加减运算时，才把每个数的符号位值同时送到ALU的双符号位中，即只在ALU中采用双符号位。所以选B

5. 

   答案与解析：

   
   答案： D
   解析：
   采用进位位判断溢出时，最高有效位进位和符号位进位的值不同时才会溢出
   

6. 

   答案与解析：

   
   答案： B
   解析：
   X₀,X₁不同会发生溢出(X₁当作第二个符号位,模4补码)

7. 

   答案与解析：

   
   答案： D
   解析：
   1位乘需要向右移动N次，加上原来的N位，一共2N位数值位
   乘积的结果需要加上1位符号位，所以一共2N+1位

8. 

   答案与解析：

   
   答案： B
   解析：
   B说的对

9. 

   答案与解析：

   
   答案： B
   解析：
   不管补码减法还是无符号数减法，都是用被减数加上减数的负数的补码来实现的。x-y=x+[-y]_补
   x的输入信息都一样，忽略
   [-y]_补 = 1101 1010
   其中，由于这是减法，所以SUB中为1，所以进位信息为[-y]_补-1=[-y]_反=1101 1001，SUB(进位信息)=1

10. 

    答案与解析：

    
    答案： D
    解析：
    C语言的数据在内存中为补码形式
    x的机器数为0...(26个0)01...(6个1)1=0000007F H(正数原反补一样)
    y的机器数为10...(11个0)01001=补=>1...(12个1) 0111=FFF7 H
    z的机器数将前两个加一块=0...076 H(最高位进位1自然丢弃)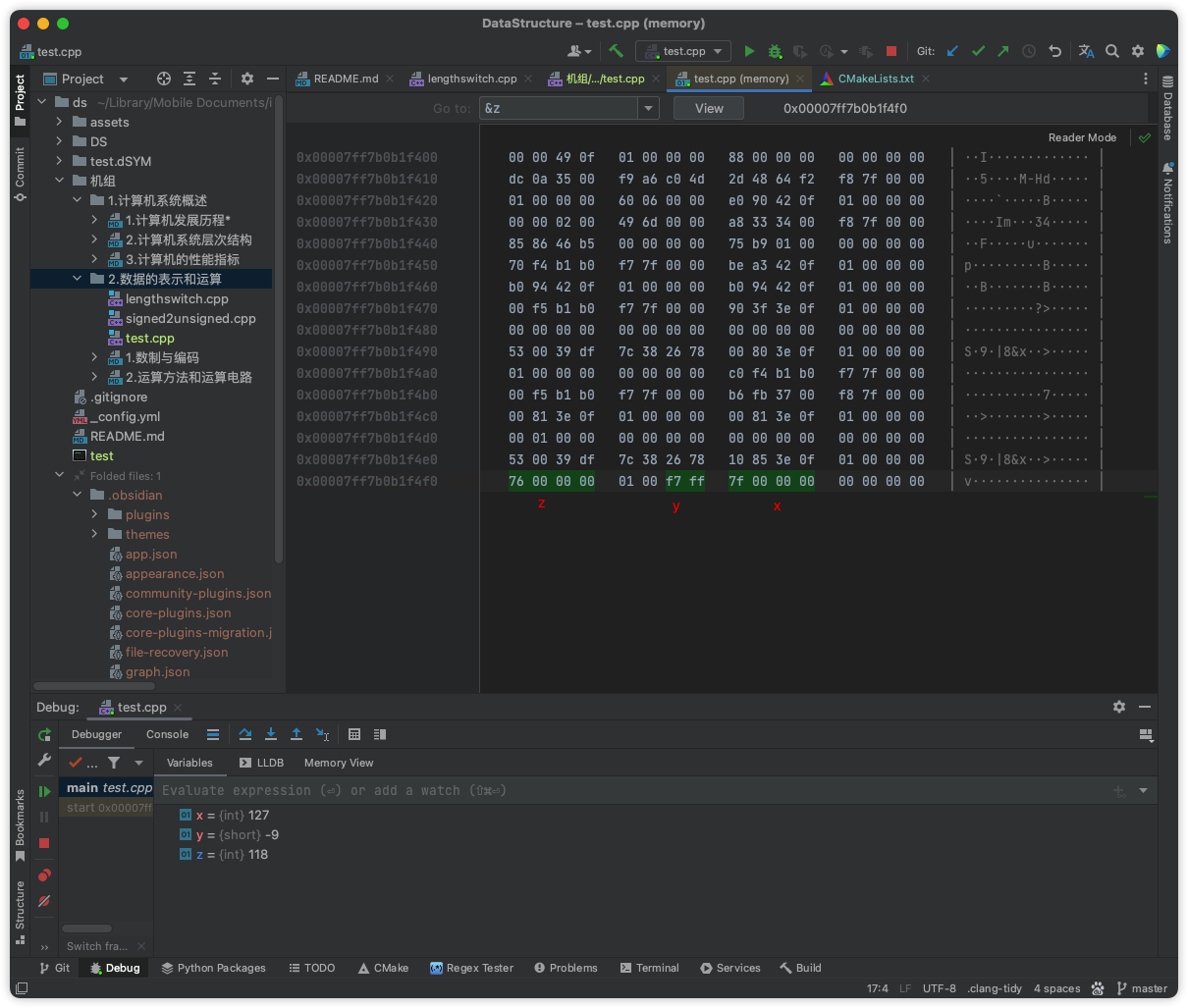 （可能我电脑默认小端存储，题目默认大端存储）

11. 

    答案与解析：

    
    答案： D
    解析：
    int a占4B，char b占1B，short c占2B
    数据按边界对齐：起始地址能被自身长度整除
    结构体成员边界对齐规则：如果一个结构体内有某些成员，一行的大小是结构体内最大元素的大小，其他元素对齐
    

12. 

    答案与解析：

    
    答案： A
    解析：
    2x=x算术左移一位=1 1101000
    y/2=y算术右移一位=1 1011000
    相加得到1 1000000,均无溢出

13. 

    答案与解析：

    
    答案： C
    解析：
    8位定点补码表示范围是-128～127
    x+y=78；-x+y=-128；x-y=128；-x-y=-78
    显然只有x-y溢出

14. 

    答案与解析：

    
    答案： D
    解析：
    [si]_补=1000 0000 0000 0001(最前面的1是符号位)
    1000 0000 0000 0001(把符号位当数值位)=2¹⁵+1=32768+1=32769

15. 

    答案与解析：

    
    答案： C
    解析：
    x转原码，第一位F换成二进制第一位肯定是1，所以一定是负数，后面的F转原码后一定是0，所以只需要看DF H的二进制转原码
    DF H = 1101 1111B = 0010 0001(原码)=33
    y的第一位是0(正数),原反补一致，所以y=65
    [-y]_补=[...0100 0001]_补=FFFF FFBF(前边的部分无所谓，只需关注16进制的后两位)
    x和-y补码的最后一位相加=F+F = 1E，所以选E

16. 

    答案与解析：

    
    答案： A
    解析：
    R1的原码为1000 ... 0001，R2的原码为1000 ... 0001 0000
    R1-R2=1000 ... 0001 + 0000 ... 0001 0000，没有发生进位=>CF=0，没有发生溢出=>OF=0

17. 

    答案与解析：

    
    答案： A
    解析：
    short是16位，所以usi的机器码是1111 1111 1111 1111
    第一位当作符号位后，[si]_补=1111 1111 1111 1111，所以[si]_原=1000 ... 0001=-1

18. 

    答案与解析：

    
    答案： D
    解析：