变分自编码器(VAE)

一、变分自编码器概述

变分自编码器（Variational Auto-Encoders，VAE）作为深度生成模型的一种形式，是由 Kingma 等人于 2014 年提出的基于变分贝叶斯（Variational Bayes，VB）推断的生成式网络结构。与传统的自编码器通过数值的方式描述潜在空间不同，它以概率的方式描述对潜在空间的观察，在数据生成方面表现出了巨大的应用价值。VAE一经提出就迅速获得了深度生成模型领域广泛的关注，并和生成对抗网络（Generative Adversarial Networks，GAN）被视为无监督式学习领域最具研究价值的方法之一，在深度生成模型领域得到越来越多的应用。

二、变分自编码器原理

传统的自编码器模型主要由两部分构成：编码器（encoder）和解码器（decoder）。如下图所示：

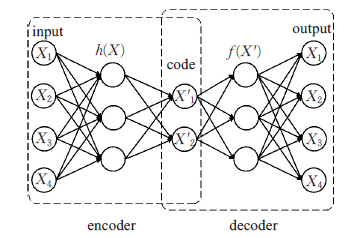
在上面的模型中，经过反复训练，我们的输入数据X最终被转化为一个编码向量\(X’\)， 其中\(X’\)的每个维度表示一些学到的关于数据的特征，而\(X’\)在每个维度上的取值代表X在该特征上的表现。随后，解码器网络接收\(X’\)的这些值并尝试重构原始输入。

举一个例子来加深大家对自编码器的理解：

假设任何人像图片都可以由表情、肤色、性别、发型等几个特征的取值来唯一确定，那么我们将一张人像图片输入自动编码器后将会得到这张图片在表情、肤色等特征上的取值的向量\(X’\)，而后解码器将会根据这些特征的取值重构出原始输入的这张人像图片。

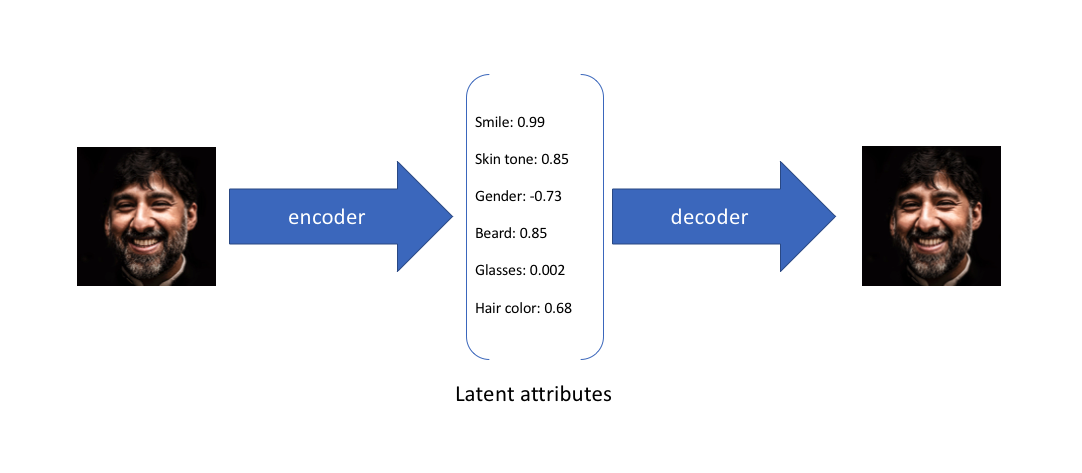
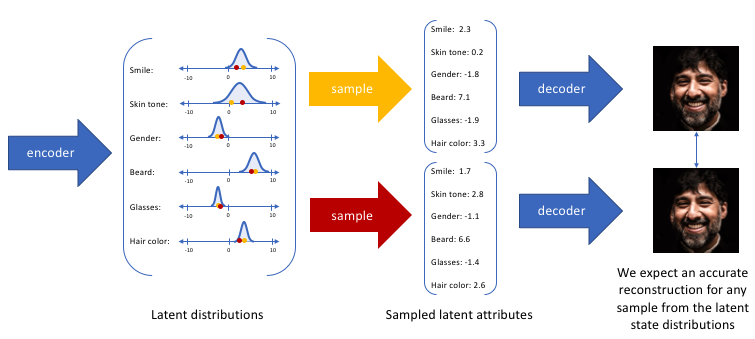
在上面的示例中，我们使用单个值来描述输入图像在潜在特征上的表现。但在实际情况中，我们可能更多时候倾向于将每个潜在特征表示为可能值的范围。例如，如果输入蒙娜丽莎的照片，将微笑特征设定为特定的单值（相当于断定蒙娜丽莎笑了或者没笑）显然不如将微笑特征设定为某个取值范围（例如将微笑特征设定为x到y范围内的某个数，这个范围内既有数值可以表示蒙娜丽莎笑了又有数值可以表示蒙娜丽莎没笑）更合适。而变分自编码器便是用“取值的概率分布”代替原先的单值来描述对特征的观察的模型，如下图的右边部分所示，经过变分自编码器的编码，每张图片的微笑特征不再是自编码器中的单值而是一个概率分布。

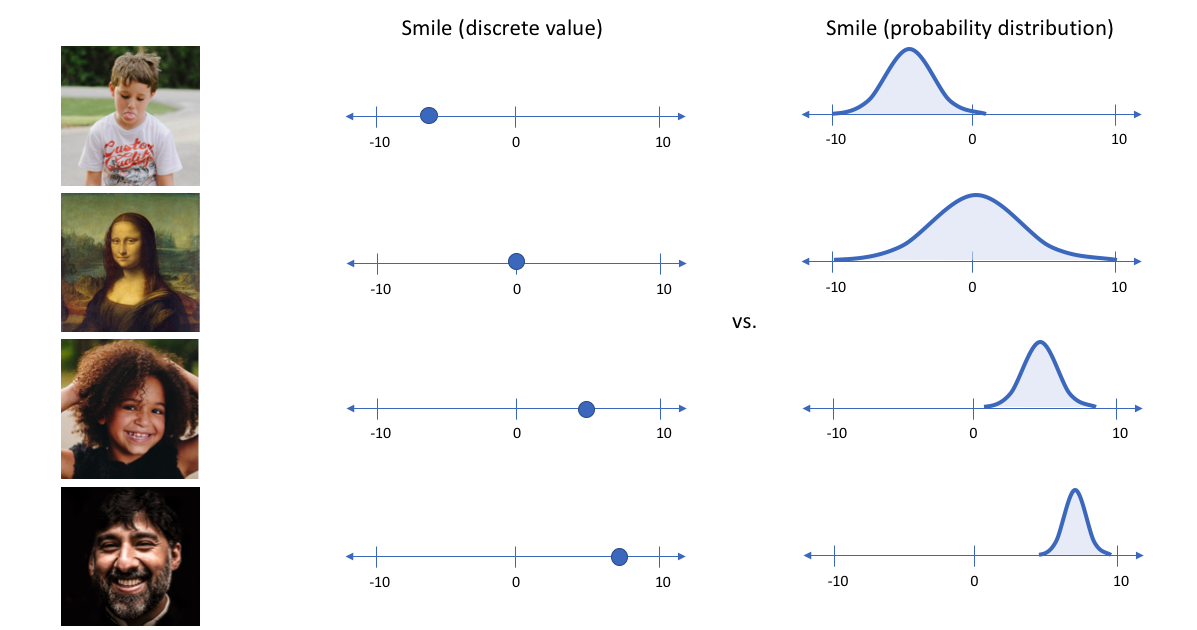
通过这种方法，我们现在将给定输入的每个潜在特征表示为概率分布。当从潜在状态解码时，我们将从每个潜在状态分布中随机采样，生成一个向量作为解码器模型的输入。

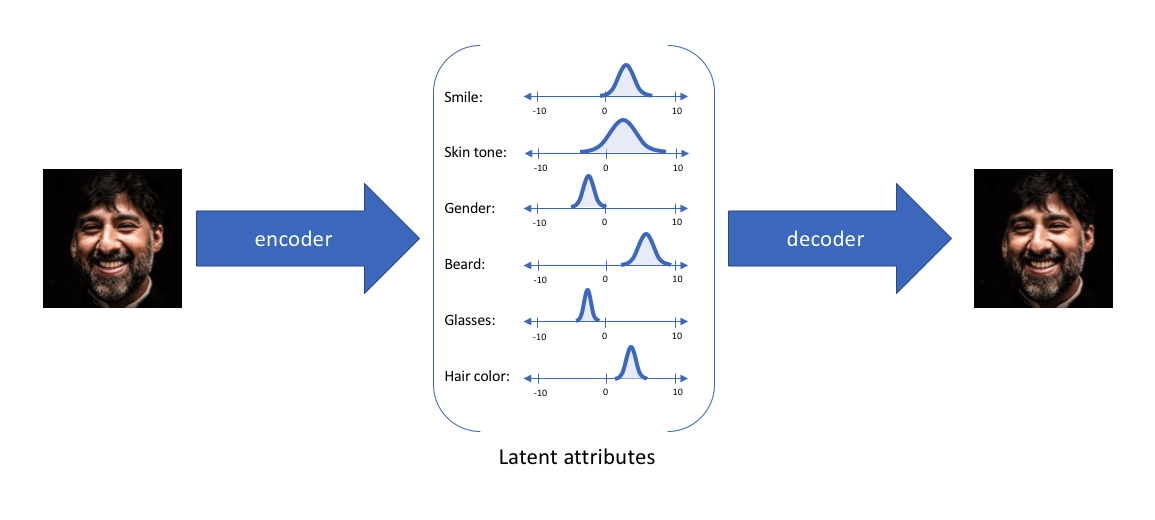
通过上述的编解码过程，我们实质上实施了连续，平滑的潜在空间表示。对于潜在分布的所有采样，我们期望我们的解码器模型能够准确重构输入。因此，在潜在空间中彼此相邻的值应该与非常类似的重构相对应。

以上便是变分自编码器构造所依据的原理，我们再来看一看它的具体结构。

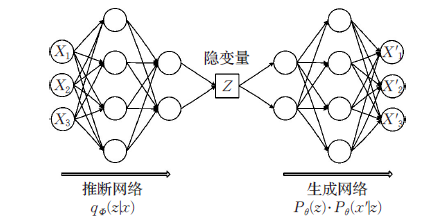
如上图所示，与自动编码器由编码器与解码器两部分构成相似，VAE利用两个神经网络建立两个概率密度分布模型：一个用于原始输入数据的变分推断，生成隐变量的变分概率分布，称为推断网络；另一个根据生成的隐变量变分概率分布，还原生成原始数据的近似概率分布，称为生成网络。

假设原始数据集为\(X = \{x_i\}_{i=1}^N\)，每个数据样本\(x_i\) 都是随机产生的相互独立、连续或离散的分布变量，生成数据集合为 \(X'=\{x_i'\}_{i=1}^N\) ，并且假设该过程产生隐变量\(Z\) ，即\(Z\)是决定\(X\)属性的神秘原因（特征）。其中可观测变量 \(X\) 是一个高维空间的随机向量，不可观测变量 \(Z\) 是一个相对低维空间的随机向量，该生成模型可以分成两个过程：

1. 隐变量 \(Z\)?后验分布的近似推断过程, 即推断网络：

   \[ q_{\phi}(z|x) \]

2. 生成变量\(X'\)的条件分布生成过程，即生成网络：

   \[ P_\theta(z)P_\theta(x'|z) \]

尽管VAE 整体结构与自编码器AE 结构类似，但VAE 的作用原理和AE 的作用原理完全不同，VAE 的“编码器”和“解码器” 的输出都是受参数约束变量的概率密度分布，而不是某种特定的编码。

三、变分自编码器推导

在上一节中，我们已经介绍过变分自动编码器学习的是隐变量（特征）\(Z\)的概率分布，因此在给定输入数据\(X\)的情况下，变分自动编码器的推断网络输出的应该是\(Z\)的后验分布\(p(z|x)\)。 但是这个\(p(z|x)\)后验分布本身是不好求的。所以有学者就想出了使用另一个可伸缩的分布\(q(z|x)\)来近似\(p(z|x)\)。通过深度网络来学习\(q(z|x)\)的参数，一步步优化\(q\)使其与\(p(z|x)\)十分相似，就可以用它来对复杂的分布进行近似的推理。

为了使得\(q\)和\(p\)这两个分布尽可能的相似，我们可以最小化两个分布之间的KL散度，也许有朋友不了解什么叫KL散度，简单来说他就是衡量两个分布之间的距离，值越小两者越相近，值越大两者差距越大。

\[ min KL(q(z|x)||p(z|x)) \]

因为\(q(z|x)\)为分布函数，所以有\(\sum_zq(z|x)=1\)

所以

\[ L = log(p(x))\newline=\sum_zq(z|x)log(p(x))\newline=\sum_zq(z|x)log(\frac{p(z,x)}{p(z|x)})\newline=\sum_zq(z|x)log(\frac{p(z,x)}{p(z|x)}\frac{q(z|x)}{p(z|x)})\newline=\sum_zq(z|x)log(\frac{p(z,x)}{p(z|x)}) + \sum_zq(z|x)log(\frac{q(z|x)}{p(z|x)})\newline =L^v + D_{KL}(q(z|x)||p(z|x)) \]

因为KL散度是大于等于0的

所以\(L\geqq L^v\),\(L^v\)被称为\(L\)的下界。

又因为\(p(x)\)是固定的，即\(L\)是一个定值，我们想要最小化\(p\)和\(q\)之间的散度的话，便应使得\(L^v\)最大化。

\[ L^v=\sum_zq(z|x)log(\frac {p(z,x)}{q(z|x)}\newline=\sum_zq(z|x)log(\frac{p(x|z)p(z)}{q(z|x)}\newline=\sum_zq(z|x)log(\frac{p(z)}{q(z|x)})+\sum_zq(z|x)log(p(x|z))\newline L^v=-D_{KL}(q(z|x)||p(z)) + E_{q(z|x)}(log(p(x|z))) \]

要最大化这个，也就是说要最小化q(z|x)和p(z)的KL散度，同时最大化上式右边式子的第二项。因为q（z|x）是利用一个深度网络来实现的，我们事先假设z本身的分布是服从高斯分布，这也就是要让推断网络（编码器）的输出尽可能的服从高斯分布。

已知P（z）是服从正态高斯分布的：

\[ p_\theta(z)=N(0,1)\newline q_\phi(z|x) = N(z;u_z(x,\phi),\sigma_z^2(x,\phi) \]

然后依据KL散度的定义，??\(L^v\)第一项可以分解为如下：（将第一项称为\(L_1\)）

\[ L_1 = \int q_\phi(z|x)log p(z)dz - \int q_phi(z|x)log q_\phi(z|x)dz \]

然后分成两项分别对其进行分别求导：

\[ \int q_phi(z|x)log q_\phi(z|x)dz \newline = \int N(z;u,\sigma^2)log N(z;0,1)dz \newline = E_{z\sim N(u,\sigma^2)}[log N(z;0,1)] \newline = E_{z\sim N(u,\sigma^2)}[log(\frac{1}{\sqrt{2\pi}}e^{\frac{(z)^2}{2}})] \newline = -\frac12 log2\pi - \frac12E_{z\sim N(u,\sigma^2)}[z^2] \newline = -\frac12log 2\pi - \frac12(u^2+\sigma^2) \]

\[ \int q_phi(z|x)log q_\phi(z|x)dz \newline = \int N(z;u,\sigma^2)log N(z;u,\sigma^2)dz \newline = E_{z\sim N(u,\sigma^2)}[log N(z;u,\sigma^2)] \newline = E_{z\sim N(u,\sigma^2)}[log(\frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{(z-u)^2}{2\sigma^2}})] \newline = -\frac12 log2\pi - \frac12 log\sigma^2 - \frac12E_{z\sim N(u,\sigma^2)}[(z-u)^2] \newline = -\frac12log 2\pi - \frac12(log \sigma^2+1) \]

所以最后得出\(L_1\)的值:

\[ L_1 = \frac12\sum_{j=1}^J[1+log((\sigma_j)^2) - (u_j)^2 - (\sigma_j)^2] \]

我们的目的就是将上面这个式子最大化。

接下来我们来最大化\(L^v\)的右边部分?\(L_2\)?，关于\(p\)和\(q\)的分布如下：

\[ q_\phi(z|x) = N(u(x,\phi),\sigma^2(x,\phi)\cdot I)\newline p_\phi(x|z) = N(u(z,\theta),\sigma^2(z,\theta)\cdot I) \]

对于对数似然期望的求解会是一个十分复杂的过程，所以采用MC算法，将\(L_2\)等价于：

\[ L_2 = E_{q(z|x)}(log(p(x|z)))\approx\frac1L\sum_{l=1}^Llog p(x|z^{(l)}) \]

其中，

\[ z^{(l)}\sim q(z|x) \]

最后，根据上面假设的分布，我们不难计算出使得取最大值时的\(q_\phi(z|x)\)，至此我们的推断网络（编码器）部分推导完毕。

参考文献

[1]Kingma D P, Welling M. Auto-Encoding Variational Bayes[J]. stat, 2014, 1050: 10.

[2]jeremyjordan，Introduction to autoencoders

[3]yuxiangyu,从自编码器到变分自编码器（其二）

[4][super多多](https://link.zhihu.com/?target=https%3A//me.csdn.net/weixin_40955254),Auto-Encoding Variational Bayes学习笔记

转载自：一文理解变分自编码器（VAE）