Link Prediction of Textual Edge Graphs
本文最后更新于 2024年6月14日 晚上
Link Prediction of Textual Edge Graphs

摘要
文本边缘图(TEG, 边缘上具有富文本的网络)封装了大量关系和上下文信息。但是现有的研究方法分为基于GNN和基于LLM两类,都有些问题。本文提出一种新的框架(LINK2DOC)专门用于TEG上进行链路预测(预测两个节点之间是否存在链接)。
graph LR
A(("A<br>文本描述: Node A details")) -- "文本描述: Edge AB details" --- B(("B<br>文本描述: Node B details"))
A -- "文本描述: Edge AC details" --- C(("C<br>文本描述: Node C details"))
B -- "文本描述: Edge BD details" --- D(("D<br>文本描述: Node D details"))
C -- "文本描述: Edge CD details" --- D
文本边缘图
创新点
LINK2DOC 通过将节点对之间的邻居信息总结为类人类编写的文档,并利用自监督学习模型增强GNN的文本理解能力。
结论
在四个真实世界数据集上的实验表明,LINK2DOC 在链接预测任务中的表现优于现有的边缘感知GNNs和预训练语言模型。
研究问题
基于LLM的问题:容易丢失图形的结构信息
基于GNN的问题:无法解释TEG中可能发生的复杂交互
研究目标:提出一种新框架(LINK2DOC),旨在解决现有方法的不足,更好的进行TEG上的链路预测。
研究方法
LINK2DOC
- 连贯的文档组合,用通俗易懂的人话来描述节点对之间局部的拓扑信息,保留语义和拓扑信息
- 自监督学习模块,用自监督学习模型增强GNN语言处理能力
转换图
- 用于捕捉和表示TEG中两个节点之间的所有可能的路径
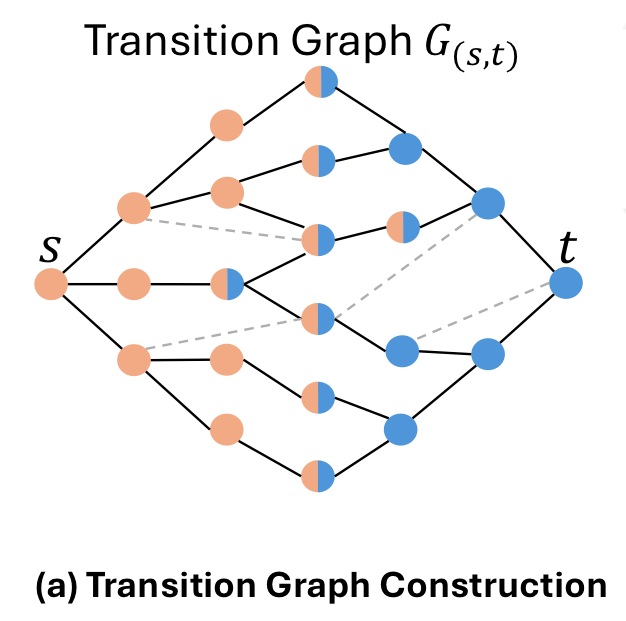
- 定义:对于TEG中的任意两个实体(节点) \((s, t)\),从\(s\)到\(t\)的所有路径共同形成一个\((s, t)\)的转换图,用\(G(s, t)\)表示。分别用\(m\)和\(n\)表示\(G(s,t)\)中的节点数和边数。路径长度上限可以用整数\(K\)来设定,通常可以将其设置为TEG的直径。
- 构建方法:
- 广度优先搜索(BFS)
- 从源节点\(s\)开始,执行BFS来探索到目标节点\(t\)的所有路径
- BFS的深度可以设置为转换图直径的一半,以确保覆盖到足够的局部领域信息
- 提取局部结构
- 提取源节点\(s\)和目标节点\(t\)的局部结构,分别记为\(G_s\)和\(G_t\)
- 分别对源节点\(s\)和目标节点\(t\)进行BFS,提取他们各自的深度为\(L\)的局部结构,
- \(s\)进行BFS时,深度小于等于\(L\)(为了\(G_s\)和\(G_t\)都能各自覆盖其近邻信息以及足够数量的节点,\(L\)通常设置为\(G(s,t)\)直径的一半)就把节点染橙色(仅论文示意图),\(t\)同理染成蓝色,两边都染色就成了两种颜色的节点
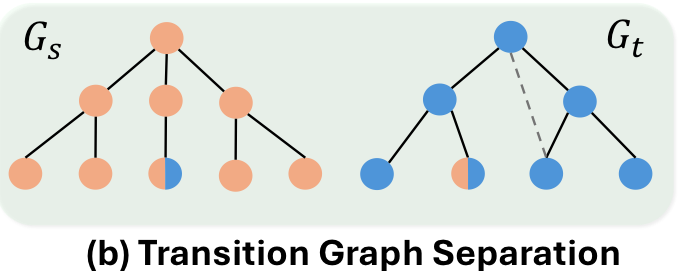
- 提取源节点\(s\)和目标节点\(t\)的局部结构,分别记为\(G_s\)和\(G_t\)
- 处理隐藏边
- 在BFS树中,某些边可能不会被直接探索到(例如,由于搜索深度限制或边不存在于BFS树中)。
- 识别这些隐藏边,并在转换图中适当地表示它们,以确保转换图的完整性。
- 合并转换图
- 将\(G_s\)和\(G_t\)合并为一个完整的转换图\(G(s, t)\),这个图包含了从\(s\) 到\(t\) 的所有路径和边
- 广度优先搜索(BFS)
转换文档构建
用于整合语义和拓扑信息
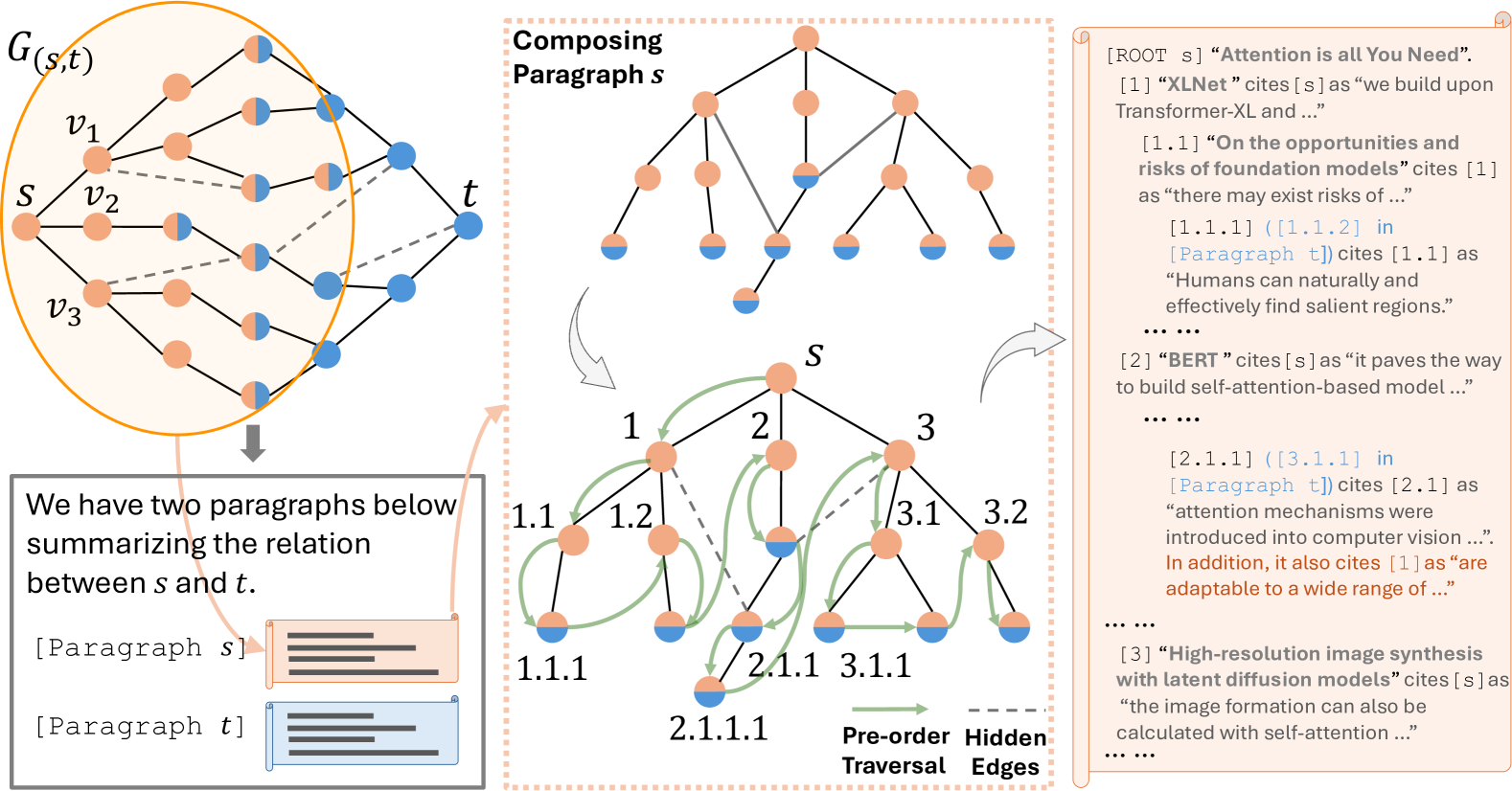
构建方法:
先得到上一步的转换图\(G(s,t)\)
使用前序遍历来分别遍历\(G_s\)和\(G_t\)中的节点,并为每个节点分配文档中的章节和小节序号,如下图
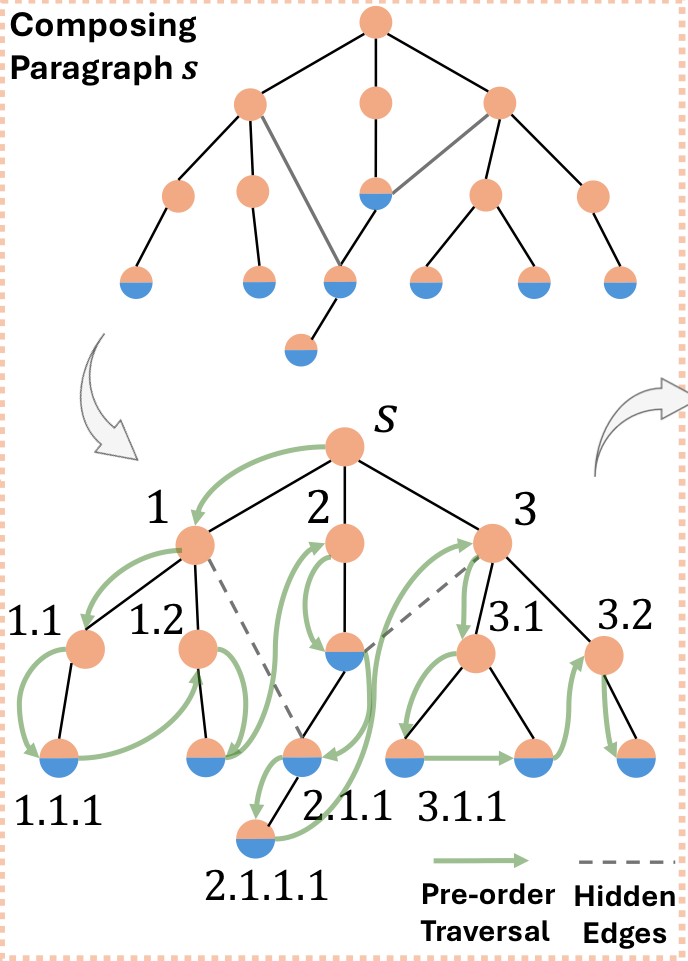
识别并添加那些在局部结构中不直接出现,但在转换图中存在的隐藏边
识别 \(G_s\)和 \(G_t\) 中的共享节点,这些节点在转换文档中需要有交叉引用,以显示它们在不同局部结构中的连接
最终将\(s\)和\(t\)的局部结构段落合并为一个统一的文档,确保文档不仅描述孤立的节点,还突出了他们之间的相互连接。

自监督学习模块
- 使用预训练模型PLM来处理转换文档\(d_{(s,t)}\),以保持文本的完整性,得到文档的潜在表示\(\widetilde h_{(s,t)} = f_{LM}(d_{(s,t)})\)
- 通过GNN处理转换图中的图结构和边文本信息,生成表示\(h_{(s,t)} = g(f_{GNN}(G_s) \oplus f_{GNN}(G_t))\)
- 使用加权交叉熵损失对齐\(\widetilde h\)和\(h\),\(\ell_{KD} = -\mathbb{E}\left[\log \frac{\exp\left(sim(\widetilde h_{(s, t)}, h_{(s, t)})/\tau\right)}{\sum^K_{k=1}\exp\left(sim(h_{(s, t)}, h_{(s, k)})/\tau\right)}\right]\)
- 最终用于预测边属性图上的链接的LLM增强表示学习的总体目标写为\(\ell = \lambda_1 \ell_{KD} + \lambda_2 \ell_{LP}\),其中\(\lambda_1\)和\(\lambda_2\)是超参数
时间复杂度
- 训练:\(O(2N+E+P^2+|E| \cdot f+N^2)\)
- 推理:\(O(|E| \cdot f + N^2)\)
Link Prediction of Textual Edge Graphs
https://tippye.github.io/2024/06/13/Link Prediction of Textual Edge Graphs/