BA模型与幂绿度分布

本文最后更新于 2024年6月14日晚上

BA无标度网络模型

BA无标度网络模型构造算法

增长:从一个具有\(m_0\)个节点的连通网络开始,每次引人一个新的节点并且连到\(m\)个已存在的节点上,这里\(m \le m_0\)。
优先连接:一个新节点与一个已经存在的节点\(i\)相连接的概率\(\prod_i\),与节点\(i\)的度\(k_i\),之间满足如下关系: \(\prod_i = \frac{k_i}{\sum_jk_j}\)

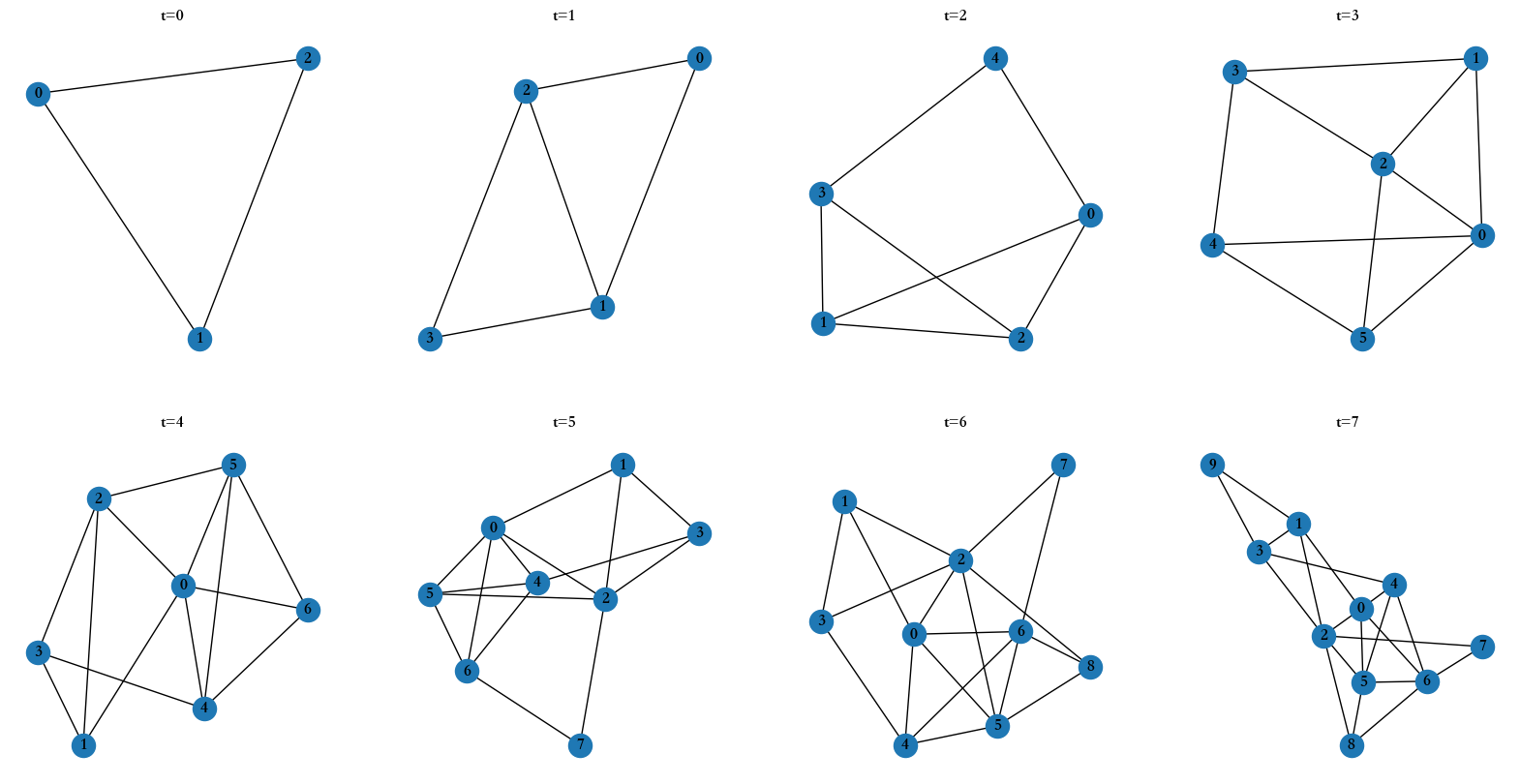
BA无标度网络的实现

先使用networkx库创建一个有\(m_0\)个节点的完全图
循环添加节点直到图的节点到\(N\)个
1. 计算选择每个节点的概率：这里使用random.choice在tmp_nodes进行选择。对于tmp_nodes，假设节点i的度为ki,则往tmp_nodes中添加ki个i,最后选择到i的概率即可变为\(\frac{k_i}{\sum_jk_j}\)。对应代码为tmp_nodes = [node for node, degree in self.G.degree() for _ in range(degree)]
2. 选择\(m\)个节点，因为上一步随机选择可能包括重复的节点，所以要使用set去重后重新选择直到选出来\(m\)个不重复的节点
3. 将新选择出来的\(m\)个节点与新节点连接，被选择的节点度都会\(+1\)，所以为了下一次新增节点，将这\(m\)个节点添加到tmp_nodes。新节点的度肯定为\(m\)，所以往tmp_nodes添加\(m\)个新节点
到此就实现了一个BA无标度网络

class BAGraph:
    def __init__(self, m0, N, m):
        """
        构建BA模型
        
        :param m0: 初始有几个节点
        :param N:  一共有几个节点
        :param m:  每次选几个节点
        """
        assert m >= m0, 'm0必须小于m'
        assert N >= m0, 'N必须大于m0'
        self.m0 = m0
        self.N = N
        self.m = m
        self.G = nx.complete_graph(m0)
        self.pk = None
        self.h = None

        # 当前节点数
        n = m0
        # 每个节点的度为多少就放几个对应节点，这样可以等价于计算度的概率
        tmp_nodes = [node for node, degree in self.G.degree() for _ in range(degree)]
        while n < N:
            new_node = n
            self.G.add_node(new_node)

            # 选择m个不重复的节点
            if len(tmp_nodes) == 0:
                # m0=1时，第一次tmp_nodes会为空，手动设置choice_nodes放0号节点，否则random.choices会报错
                choice_nodes = set([0])
            else:
                choice_nodes = set(random.choices(tmp_nodes, k=m))
            while len(choice_nodes) < m:
                choice_nodes.add(random.choice(tmp_nodes))

            for node in choice_nodes:
                self.G.add_edge(new_node, node)

            tmp_nodes.extend(choice_nodes)
            tmp_nodes.extend([new_node] * len(choice_nodes))

            n += 1

    def get_pk(self):
        """
        计算度分布
        
        :return:
        """
        if self.pk is None:
            pk = np.zeros(self.N)
            for i in range(self.N):
                pk[self.G.degree[i]] += 1
            self.pk = pk / self.N
        return self.pk

    def get_h(self):
        """
        计算幂律分布
        
        $h = \\\\frac{pk}{2*m^2}$
        :return:
        """
        if self.h is None:
            pk = self.get_pk()
            self.h = pk / (2 * self.m ** 2)
        return self.h

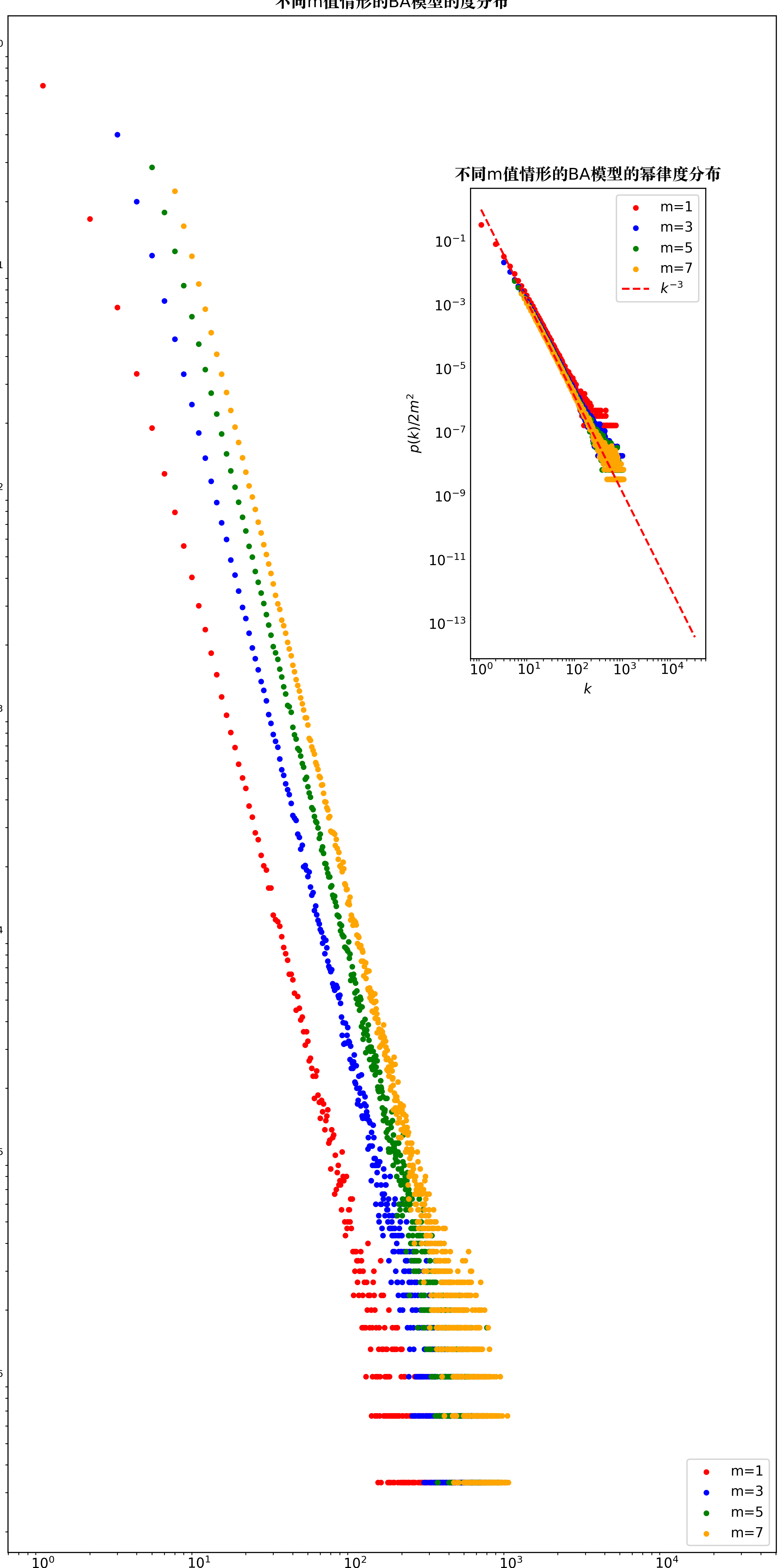
幂律度分布

BA模型具有幂律度分布且与参数\(m\)无关。下图显示的是双对数坐标下,包含\(N=t+m_0=300 000\)个节点的BA 网络的度分布\(P(k)\),并分别考虑4 个不同的\(m\)值。图中的虚线对应的是斜率为\(-2.9\)的直线,而四种情形的度分布都可以用幂指数\(\gamma_{BA} =2.9士0.1\) 的幂律分布来表示。

上述实现代码如下：

N = 30000               # 设置图的总结点数，书上给的是30w，这里为了运行时间使用了3w
sample = 100            # 样本数，对于每个m值，运行处100个图然后去均值作为度分布
m_list = [1, 3, 5, 7]   # 不同的m值
PK = np.zeros(len(m_list) * N).reshape(len(m_list), N)	# 用于存放度分布结果，因为有4个m值所以有4行，每行的长度为总节点数（度的取值范围为1～N)
H = np.zeros(len(m_list) * N).reshape(len(m_list), N)		# 用于存放幂律度分布结果
with tqdm(total=sample * len(m_list)) as pbar:
    for i, m in enumerate(m_list):
        for _ in range(sample):
            G = BAGraph(m0=m, N=N, m=m)
            PK[i] += G.get_pk()
            H[i] += G.get_h()
            pbar.update(1)
        PK[i] /= sample
        H[i] /= sample

# 后面是作图
plt.figure(figsize=(8, 16))
plt.title("不同m值情形的BA模型的度分布")
color_list = ['red', 'blue', 'green', 'orange']
for i, m in enumerate(m_list):
    plt.scatter(range(N), PK[i], s=10, label=f'm={m}', color=color_list[i])
plt.xlabel('$k$')
plt.xscale('log')
plt.ylabel('$P(k)$')
plt.yscale('log')
plt.legend(loc='lower right')

ax = plt.axes([0.6, 0.58, 0.3, 0.3])
plt.title("不同m值情形的BA模型的幂律度分布")
for i, k in enumerate(m_list):
    ax.scatter(range(N), H[i], s=10, label=f'm={k}',color=color_list[i])
    
ax.plot(range(N), np.power(np.arange(N).astype(float), -3), label='$k^{-3}$', color='red', linestyle='--')
ax.legend(loc='upper right')
ax.set(ylabel='$p(k)/2m^2$', xlabel='$k$', yscale='log', xscale='log')

plt.savefig('不同m的幂律度分布图.png', dpi=300)

BA 模型具有幂律度分布且与网络规模\(N\)无关。下图显示的是固定\(m=m_0=5\)时BA模型的度分布\(P(k)\)，网络规模分别为：N=100 000、150 000及200 000。

实现代码如下：

N_list = [100000,150000,200000]								# 不同N值列表
m = 5																					# 固定m值
PK = [np.zeros(n) for n in N_list]
H = PK.copy()
with tqdm(total=sample * len(N_list)) as pbar:
    for i, n in enumerate(N_list):
        for _ in range(sample):
            G = BAGraph(m0=m, N=n, m=m)
            PK[i] += G.get_pk()
            H[i] += G.get_h()
            pbar.update(1)
        PK[i] /= sample
        H[i] /= sample
        
plt.figure(figsize=(8, 16))
plt.title(f"不同N值情形的BA模型的度分布(m={m})")
color_list = ['red', 'blue', 'green', 'orange']
for i, n in enumerate(N_list):
    plt.scatter(range(n), PK[i], s=10, label=f'n={n}', color=color_list[i])
plt.xlabel('$k$')
plt.xscale('log')
plt.ylabel('$P(k)$')
plt.yscale('log')
plt.legend(loc='lower right')

度分布计算函数和幂律度分布计算函数

class BAGraph:
    ...
    def get_pk(self):
        """
        计算度分布
        
        :return:
        """
        # 度分布即为统计每个度的节点占总节点的分数。
        if self.pk is None:
            pk = np.zeros(self.N)		# 度的取值范围只能是1～N，不取零是因为BA模型肯定是连通图
            for i in range(self.N):	# 遍历每个节点，将pk作为哈希表
                pk[self.G.degree[i]] += 1
            self.pk = pk / self.N		# 计算出pk后要统一除以节点总数才为度分布的概率
        return self.pk

    def get_h(self):
        """
        计算幂律分布
        
        $h = \\\\frac{pk}{2*m^2}$
        :return:
        """
        if self.h is None:
            pk = self.get_pk()
            self.h = pk / (2 * self.m ** 2)	# 参考《网络科学导论》，幂律度分布为度分布/2m^2
        return self.h

#复杂网络

BA模型与幂绿度分布

https://tippye.github.io/2024/05/17/BA模型与幂绿度分布/

作者

Tippy

发布于

2024年5月17日

许可协议

Bipartite network projection and personal recommendation 上一篇

如何读一篇论文下一篇